
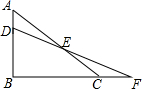
 已知:如图,在△ABC中,点D在边AB上,且AD=$\frac{1}{3}$AB.点F在边BC的延长线上,连结DF,交AC于点E,设$\frac{CF}{BF}$=k.求:$\frac{CE}{AE}$的值.
已知:如图,在△ABC中,点D在边AB上,且AD=$\frac{1}{3}$AB.点F在边BC的延长线上,连结DF,交AC于点E,设$\frac{CF}{BF}$=k.求:$\frac{CE}{AE}$的值. 分析 作CG∥AB交DF于G,如图,先由CG∥AB得到$\frac{CG}{AB}$=$\frac{CF}{BF}$=k,则CG=kAB,再由CG∥AD得到$\frac{CG}{AD}$=$\frac{CE}{AE}$,然后利用比例性质可得到$\frac{CE}{AE}$=3k.
解答 解:作CG∥AB交DF于G,如图,
∵CG∥AB,
∴$\frac{CG}{AB}$=$\frac{CF}{BF}$=k,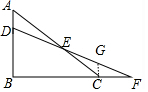
∴CG=kAB,
∵CG∥AD,
∴$\frac{CG}{AD}$=$\frac{CE}{AE}$,
而CG=kAB,AD=$\frac{1}{3}$AB,
∴$\frac{CE}{AE}$=$\frac{kAB}{\frac{1}{3}AB}$=3k.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.熟练掌握比例的性质.


科目:初中数学 来源: 题型:解答题
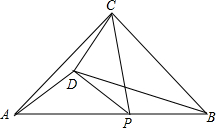 如图,在等腰直角△ABC中,点P为斜边AB上一动点(不与A、B两点重合),以CP为斜边在直线CP左侧作等腰直角△CPD.
如图,在等腰直角△ABC中,点P为斜边AB上一动点(不与A、B两点重合),以CP为斜边在直线CP左侧作等腰直角△CPD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
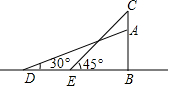 如图,小山AB的顶上有一高20m的铁塔(CA),在山脚平地上的D点,测得山顶A的仰角为30°,在E点测得塔尖C的仰角为45°(点D、E、B在一条直线上),已知DE=60m.求山高AB.(结果保留根号)
如图,小山AB的顶上有一高20m的铁塔(CA),在山脚平地上的D点,测得山顶A的仰角为30°,在E点测得塔尖C的仰角为45°(点D、E、B在一条直线上),已知DE=60m.求山高AB.(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com