
【题目】某校为了了解学生对语文、数学、英语、物理四科的喜爱程度(每人只选一科),特对八年级某班进行了调查,并绘制成如下频数和频率统计表和扇形统计图:
科目 | 频数 | 频率 |
语文 |
| 0.5 |
数学 | 12 |
|
英语 | 6 |
|
物理 |
| 0.2 |

(1)求出这次调查的总人数;
(2)求出表中![]() 的值;
的值;
(3)若该校八年级有学生1000人,请你算出喜爱英语的人数,并发表你的看法.
【答案】(1)60人;(2)a=30,b=0.2,c=0.1,d=12;(3)喜爱英语的人数为100人,看法见解析.
【解析】
(1)用喜爱英语科目的人数除以其所占比例;
(2)根据频数=频率×总人数求解可得;
(3)用八年级总人数乘以样本中喜爱英语科目人数所占比例,计算即可.
解:(1)这次调查的总人数为:6÷(36°÷360°)=60(人);
(2)a=60×0.5=30(人);b=12÷60=0.2;c=6÷60=0.1;d=0.2×60=12(人);
(3)喜爱英语的人数为1000×0.1=100(人),
看法:由扇形统计图知喜爱语文的人数占总人数的一半,是四个学科中喜爱人数最多的科目.


科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是__________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=8,AB=4,将此矩形折叠,使点B与点D重合,折痕为EF,连接BE、DF,以B为原点建立平面直角坐标系,使BC、BA边分别在x轴和y轴的正半轴上.

(1)试判断四边形BFDE的形状,并说明理由;
(2)求直线EF的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,E.F.G.H依次是各边的中点,O是四边形ABCD内一点,若四边形AEOH.四边形BFOE.四边形CGOF的面积分别为10.12.14,则四边形DHOG的面积=______.
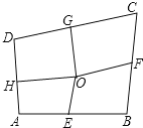
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线x与直线y垂直于点O,点B,C在直线x上,点A在直线x外,连接AC,AB得到△ABC.
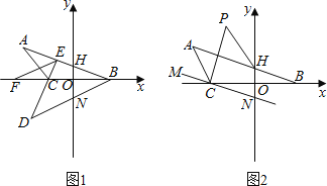
(1)将△ABC沿直线x折叠,使点A落在点D处,延长DC交AB于点E,EF平分∠AED交直线x于点F.
①若∠EFB=25°,∠DEF=10°,则∠DCF=______
②若∠ACF-∠AEF=18°,求∠EFB的度数;
(2)过点C作MN平行于AB交直线y于点N,CP平分∠BCM,HP平分∠AHY,当点C从点O沿直线x向左运动时,∠CPH的度数是否发生变化?若不变求其度数;若变化,求其变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图:
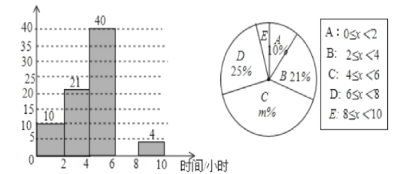
根据图中提供的信息,解答下列问题:
(1)共随机调查了___名学生,课外阅读时间在68小时之间有___人,并补全频数分布直方图;
(2)求扇形统计图中m的值和E组对应的圆心角度数;
(3)请估计该校3000名学生每周的课外阅读时间不小于6小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP 交于点O,并分别与边CD,BC 交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=0E![]() OP;③
OP;③![]() ;④当BP=1时,
;④当BP=1时,![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
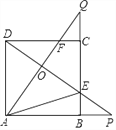
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
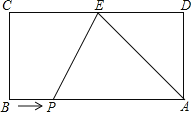
【题目】如图,已知矩形ABCD,AB=8,AD=4,E为CD边上一点,CE=5,P点从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE,设点P运动的时间为t秒,则当t的值为______时,∠PAE为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学李老师选派了班上8位同学去参加年级组的数学知识竞赛,试卷满分100分,我们将成绩中超过90分的部分记为正,低于90分的部分记为负,则这8位同学的得分如下(单位:分):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)请求出这8位同学本次数学竞赛成绩的平均分是多少?
(2)若得95分以上可以获得一等奖,请求出获得一等奖的百分比是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com