
【题目】如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B的坐标为(18,6).
(1)求直线l1,l2对应的函数表达式;
(2)点C为线段OB上一动点(点C不与点O,B重合),作CD∥y轴交直线l2于点D,设点C的纵坐标为a,求点D的坐标(用含a的代数式表示).
【答案】(1) y=-x+24;(2) D的坐标为(3a,-3a+24)
【解析】
(1)根据题意可设直线l1的表达式为y=k1x,设直线l2的表达式为y=k2x+b,将点B、点A的坐标代入直线表达式中求出系数,则可得直线表达式;
(2) 因为点C在直线l1上,已知点C的纵坐标,由直线表达式可得点C的横坐标,因为CD//y轴,所以点D的横坐标与点C的横坐标相等,将D点横坐标代入l2表达式,即可得点D的坐标.
(1)设直线l1对应的函数表达式为y=k1x,由它过点(18,6)得18k1=6,解得k1=![]()
所以直线l1对应的函数表达式为y=![]() x;
x;
设直线l2对应的函数表达式为y=k2x+b,由它过点A(0,24),B(18,6)得b=24,18k2+b=6,解得k2=-1,所以直线l2对应的函数表达式为y=-x+24.
(2)因为点C在直线l1上,且点C的纵坐标为a,所以a=![]() x.
x.
所以x=3a,故点C的坐标为(3a,a).
因为CD∥y轴,
所以点D的横坐标为3a.
因为点D在直线l2上,
所以点D的纵坐标为-3a+24.
所以点D的坐标为(3a,-3a+24).


科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
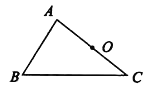
已知:如图,△ABC及AC边的中点O。
求作:平行四边形ABCD。
小敏的作法如下:
①连接BO并延长,在延长线上截取OD=BO;
②连接DA,DC.
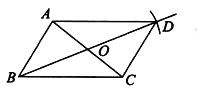
所以四边形ABCD就是所求作的平行四边形.
老师说:“小敏的作法正确.”
请回答:小敏的作法正确的理由是_________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下图回答问题: 
(1)指出小明的作业从哪一步开始出现的错误,请更正过来,并计算出正确结果;
(2)若a,b是不等式组 ![]() 的整数解(a<b),求上题{}分式的值.
的整数解(a<b),求上题{}分式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠ACB=90°,AC=BC,AD⊥CM,BE⊥CM,垂足分别为D,E,
(1)如图1, 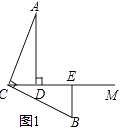
①线段CD和BE的数量关系是;
②请写出线段AD,BE,DE之间的数量关系 .
(2)如图2,上述结论②还成立吗?如果不成立,请直接写出线段AD,BE,DE之间的数量关系. 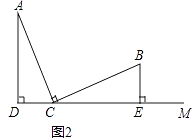
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,夜晚,小亮从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间的函数关系的图象大致为( )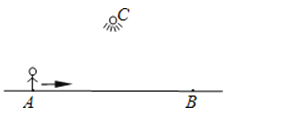
A.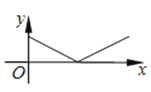
B.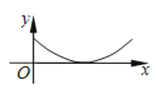
C.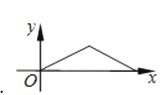
D.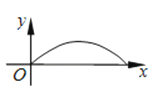
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com