
【题目】一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天,已知甲工程队铺设每天需支付工程费2000元,乙工程队铺设每天需支付工程费1500元.
(1)甲、乙两队合作施工多少天能完成该管线的铺设?
(2)由两队合作完成该管线铺设工程共需支付工程费多少元?
(3)根据实际情况,若该工程要求10天完成,从节约资金的角度应怎样安排施工?
【答案】(1)8天;(2)28000元;(3)甲、乙合干7天,剩下的乙再干3天完成任务
【解析】
(1)设甲、乙两队合作施工![]() 天能完成该管线的铺设,根据工作总量为1,列出方程解答即可;
天能完成该管线的铺设,根据工作总量为1,列出方程解答即可;
(2)由(1)的数据直接计算得出结果即可;
(3)若该工程要求10天完成,乙工程队费用低,所以乙干满10天,剩下的让甲工程队干,算出天数即可.
(1)设甲、乙两队合作施工![]() 天能完成该管线的铺设,由题意得
天能完成该管线的铺设,由题意得![]() ,解得
,解得![]() .
.
答:甲、乙两队合作施工8天能完成该管线的铺设.
(2)![]() (元).
(元).
答:两队合作完成该管线铺设工程共需支付工程费28000元.
(3)若该工程要求10天完成,乙工程队费用低,所以设乙干满10天,剩下的让甲工程队干需要![]() 天,由题意得
天,由题意得![]() ,
,
解得![]() ,
,![]() .
.
故甲、乙合干7天,剩下的乙再干3天完成任务.


科目:初中数学 来源: 题型:
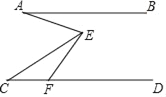
【题目】如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在全民读书月活动中,某校随机抽样调查了一部分学生本学期计划购买课外书的费用情况,根据图中的相关信息,解答下面问题;
(1)这次调查获取的样本容量是 ;
(2)由统计图可知,这次调查获取的样本数据的众数是 ;中位数是 ;
(3)求这次调查获取的样本数据的平均数;
(4)若该校共有1000名学生,根据样本数据,估计该校本学期计划购买课外书的总花费.

查看答案和解析>>
科目:初中数学 来源: 题型:
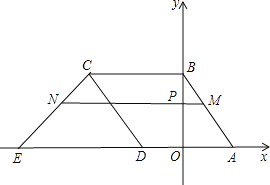
【题目】直线![]() 与x轴交于点A,与y轴交于点B,菱形ABCD如图放置在平面直角坐标系中,其中点D在x轴负半轴上,直线y=x+m经过点C,交x轴于点E.
与x轴交于点A,与y轴交于点B,菱形ABCD如图放置在平面直角坐标系中,其中点D在x轴负半轴上,直线y=x+m经过点C,交x轴于点E.
①请直接写出点C、点D的坐标,并求出m的值;
②点P(0,t)是线段OB上的一个动点(点P不与O、B重合),经过点P且平行于x轴的直线交AB于M、交CE于N.设线段MN的长度为d,求d与t之间的函数关系式(不要求写自变量的取值范围);
③点P(0,t)是y轴正半轴上的一个动点,为何值时点P、C、D恰好能组成一个等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由相同的花盆按一定的规律组成的形如正多边形的图案,其中第1个图形共有6个花盆,第2个图形一共有12个花盆,第3个图形一共有20个花盆,…,则第10个图形中花盆的个数为( )

A. 110B. 120C. 132D. 140
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y=![]() (x>0)的图象经过矩形的对称中点E,且与边BC交于点D,若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,则此直线的解析式为_____.
(x>0)的图象经过矩形的对称中点E,且与边BC交于点D,若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,则此直线的解析式为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
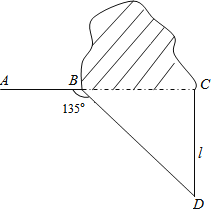
【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(![]() ≈1.414,精确到1米)
≈1.414,精确到1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】淮安日报社为了了解市民“获取新闻的主要途径”,开展了一次抽样调查,根据调查结果绘制了如图三种不完整的统计图表.

请根据图表信息解答下列问题:
(1)统计表中的m= ,n= ;
(2)并请补全条形统计图;
(3)若该市约有80万人,请你估计其中将“电脑上网”和“手机上网”作为“获取新闻的主要途径”的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一边长为36cm的正方形硬纸板进行适当的剪裁,折成一个长方体盒子(纸板的厚度忽略不计)
(1)如图,若在正方形硬纸板的四角各剪一个同样大小的正方形,将剩余部分折成一个无盖的长方体盒子.
①要使折成的长方体盒子的底面积为676cm2,那么剪掉的正方形的边长为多少?
②折成的长方形盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形的边长;如果没有,说明理由.
(2)若在正方形硬纸板的四周剪掉一些矩形(即剪掉的矩形至少有一条边在正方形硬纸板的边上),将剩余部分折成一个有盖的长方体盒子,若折成的一个长方体盒子的表面积为880cm2,求此时长方体盒子的长、宽、高(只需求出符合要求的一种情况)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com