
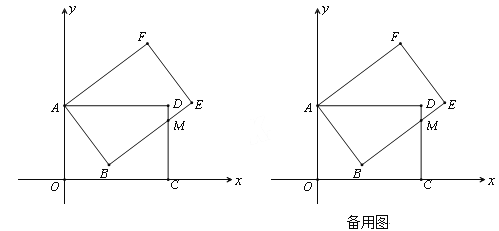
【题目】矩形AOCD绕顶点A(0,5)逆时针方向旋转,当旋转到如图所示的位置时,边BE交边CD于M,且ME=2,CM=4.
(1)求AD的长;
(2)求经过A、B、D三点的抛物线的解析式;
(3)在直线AM下方,(2)中的抛物线上是否存在点P,使S△PAM =![]() ?若存在,求出P点坐标;若不存在,请说明理由.
?若存在,求出P点坐标;若不存在,请说明理由.
【答案】(1)AD=7;(2)![]() ;(3)P点坐标为(3,1)、(
;(3)P点坐标为(3,1)、(![]() ,
,![]() )
)
【解析】试题分析: (1)作BP⊥AD于P,BQ⊥MC于Q,根据旋转的性质得AB=AO=5,BE=OC=AD,∠ABE=90°,利用等角的余角相等得∠ABP=∠MBQ,可证明Rt△ABP∽Rt△MBQ得到![]() ,设BQ=PD=x,AP=y,则AD=x+y,所以BM=x+y-2,利用比例性质得到PBMQ=xy,而PB-MQ=DQ-MQ=DM=1,利用完全平方公式和勾股定理得到52-y2-2xy+(x+y-2)2-x2=1,解得x+y=7,则BM=5,BE=BM+ME=7,所以AD=7;
,设BQ=PD=x,AP=y,则AD=x+y,所以BM=x+y-2,利用比例性质得到PBMQ=xy,而PB-MQ=DQ-MQ=DM=1,利用完全平方公式和勾股定理得到52-y2-2xy+(x+y-2)2-x2=1,解得x+y=7,则BM=5,BE=BM+ME=7,所以AD=7;
(2)由AB=BM可判断Rt△ABP≌Rt△MBQ,则BQ=PD=7-AP,MQ=AP,利用勾股定理得到(7-MQ)2+MQ2=52,解得MQ=4(舍去)或MQ=3,则BQ=4,根据三角形面积公式和梯形面积公式,利用S阴影部分=S梯形ABQD-S△BQM进行计算即可;然后利用待定系数法求直线AM的解析式.先确定B(3,1),然后利用待定系数法求抛物线的解析式;
(3)当点P在线段AM的下方的抛物线上时,作PK∥y轴交AM于K,如图2设P(x,![]() x2-
x2-![]() x+5),则K(x,-
x+5),则K(x,-![]() x+5),则KP=-
x+5),则KP=-![]() x2+
x2+![]() x,根据三角形面积公式得到
x,根据三角形面积公式得到![]() (-
(-![]() x2+
x2+![]() x)7=
x)7=![]() ,解得x1=3,x2=
,解得x1=3,x2=![]() ,于是得到此时P点坐标为(3,1)、(
,于是得到此时P点坐标为(3,1)、(![]() ,
,![]() );再求出过点(3,1)与(
);再求出过点(3,1)与(![]() ,
,![]() )的直线l的解析式为y=-
)的直线l的解析式为y=-![]()
![]() ,则可得到直线l与y轴的交点A′的坐标为(0,
,则可得到直线l与y轴的交点A′的坐标为(0,![]() ),所以AA′=
),所以AA′=![]() ,然后把直线AM向上平移
,然后把直线AM向上平移![]() 个单位得到l′,直线l′与抛物线的交点即为P点,由于A″(0,
个单位得到l′,直线l′与抛物线的交点即为P点,由于A″(0,![]() ),则直线l′的解析式为y=-
),则直线l′的解析式为y=-![]() x+
x+![]() ,再通过解方程组
,再通过解方程组 得P点坐标.
得P点坐标.
试题解析:
解:⑴ 如图1,连接AM,

在矩形AOCD中,∠AOC=∠ADC=90°,AD=OC,CD=AO=5,
∵CM=4,
∴DM=1,
由旋转,得∠B=∠AOC =90°,BE=OC,AB=AO=5,
设BE=OC= AD=x,
在Rt△ADM中,AM2=x2+1,
在Rt△ABM中,AM2=(x-2) 2+25,
∴x2+1=(x-2) 2+25,解得x=7,
∴AD=7.
⑵ 如图2,过点B作x轴的平行线,交AO于G,交DC于H,
则 ∠AGB=∠BHM =90°,
∴ ∠ABG+∠BAG =90°,
∵ ∠ABE=90°,
∴ ∠ABG+∠MBH =90°,
∴ ∠BAG =∠MBH ,
∵ AB=BM=5,
∴ △AGB≌△BHM(AAS),
∴ BH=AG,MH=BG,
设MH=BG=n,则DH=n+1,∴BH=AG=n+1,
∵ GH=OC=AD=7,
∴ n+(n+1)=7,
∴ n=3,
∴ AG=4,BG=3,
∵ A(0,5),
∴ 点B的坐标为(3,1),
设经过A、B、D三点的抛物线的解析式为y=ax+bx+5,将B(3,1),
D(7,5)代入,得
![]() 解得
解得
∴y=![]() x2-
x2-![]() x+5.
x+5.

图2
⑶ 存在.
设直线AM的解析式为y=kx+5,将M(7,4)代入,得k=![]() ,
,
∴y=-![]() x+5,
x+5,
∵点P在线段AD的下方的抛物线上,作PK∥y轴交AM于K,
设P(x,![]() ),则K(x,
),则K(x,![]() ),
),
∴KP=![]() ﹣
﹣![]() =
=![]() ,
,
∵S△PAM=![]() ,
,
∴![]()
![]() 7=
7=![]() ,
,
整理得7x2﹣46x+75=0,
解得x1=3,x2=![]() ,
,
此时P点坐标为(3,1)、(![]() ,
,![]() ).
).
点睛: 本题考查了几何变换综合题:熟练掌握旋转的性质、矩形的性质和三角形全等于相似的判定与性质;会利用待定系数法求函数解析式;理解坐标与图形性质;会进行代数式的变形.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,根据图中信息解答下列问题:
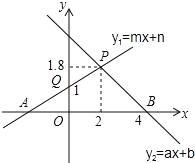
(1)关于x的不等式ax+b>0的解集是 ;
(2)关于x的不等式mx+n<1的解集是 ;
(3)当x满足 的条件时,y1y2;
(4)当x满足 的条件时,0<y2<y1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC内接于⊙O,P是![]() 上任一点(点P不与点A、B重合),连AP、BP,过点C作CM∥BP交PA的延长线于点M.
上任一点(点P不与点A、B重合),连AP、BP,过点C作CM∥BP交PA的延长线于点M.
(1)填空:∠APC=____ 度,∠BPC=____度;
(2)求证:△ACM≌△BCP;
(3)若PA=1,PB=2,求梯形PBCM的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店今年1月份的销售额是2万元,3月份的销售额是3.38万元.
(1)求从1月份到3月份,该商店销售额平均每月的增长率;
(2)如果该商店4月份销售额增长率保持不变,销售额能否达到4.5万元,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
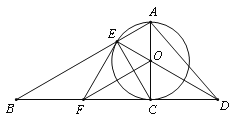
【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,作OF∥AB交BC于点F,连接EF.
(1)求证:OF⊥CE
(2)求证:EF是⊙O的切线;
(3)若![]() O的半径为3,∠EAC=60°,求AD的长.
O的半径为3,∠EAC=60°,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.
(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;
(2)当点P在线段DB上(不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;
(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种竹制躺椅如图①所示,其侧面示意图如图②③所示,这种躺椅可以通过改变支撑杆CD的位置来调节躺椅舒适度.假设AB所在的直线为地面,已知AE=120 cm,当把图②中的支撑杆CD调节至图③中的C′D的位置时,∠EAB由20°变为25°.
(1)你能求出调节后该躺椅的枕部E到地面的高度增加了多少吗?(结果精确到0.1 cm,参考数据:sin 20°≈0.342 0,sin 25°≈0.422 6)
(2)已知点O为AE的一个三等分点,根据人体工程学,当点O到地面的距离为26 cm时,人体感觉最舒适.请你求出此时枕部E到地面的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
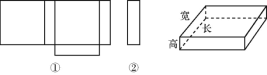
【题目】小明在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了几条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:已知这个长方体纸盒高为20 cm,底面是一个正方形,并且这个长方体纸盒所有棱长的和是880 cm,求这个长方体纸盒的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com