
【题目】如图,在平面直角坐标系中,直线![]() 与x轴,y轴分别交于点A,点B,抛物线
与x轴,y轴分别交于点A,点B,抛物线![]() 经过A,B与点
经过A,B与点![]() .
.

(1)求抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A,B重合),过点P作x轴的垂线,垂足为D,交线段AB于点E.设点P的横坐标为m.
①求![]() 的面积y关于m的函数关系式,当m为何值时,y有最大值,最大值是多少?
的面积y关于m的函数关系式,当m为何值时,y有最大值,最大值是多少?
②若点E是垂线段PD的三等分点,求点P的坐标.
【答案】(1)![]() ;(2)①解析式
;(2)①解析式![]() ,当m=1时y有最大值,最大值是3;②P(2,3)或P(
,当m=1时y有最大值,最大值是3;②P(2,3)或P(![]() )
)
【解析】
(1)根据“直线![]() 与x轴,y轴分别交于点A,点B”可求A,B坐标,再将A,B,C三点坐标代入二次函数解析式即可求出a,b,c的值,从而得出答案;
与x轴,y轴分别交于点A,点B”可求A,B坐标,再将A,B,C三点坐标代入二次函数解析式即可求出a,b,c的值,从而得出答案;
(2)①根据已知可得点P坐标,从而可求点E坐标,根据两点之间的距离公式可知PE的代数式,再根据三角形的面积公式即可得出结论;②分当PE=2ED时,当2PE=ED两种情况,列方程求解即可得出结论.
解:(1)∵直线![]() 与x轴,y轴分别交于点A,点B
与x轴,y轴分别交于点A,点B
∴A(3,0),B(0,3)
将A(3,0),B(0,3),C(-1,0)代入到![]() 中有
中有
 解得
解得
∴抛物线的解析式为![]() ;
;
(2)①∵点P的横坐标为m,且在抛物线上
∴点P的坐标为(m,![]() )
)
∵PD⊥x轴
∴点E的坐标是(m,-m+3)
∴![]()
∴![]()
∴y关于m的解析式为:![]()
∵![]()
∴当m=1时,y有最大值,最大值是3;
②当PE=2ED时,
即![]()
解得:m=2或m=3(不符合题意舍去);
当2PE=ED时
即![]()
整理得![]()
解得:![]() ,m=3(不符合题意舍去)
,m=3(不符合题意舍去)
将点m=2或m=![]() 代入抛物线解析式
代入抛物线解析式
∴点P(2,3)或P(![]() )
)


科目:初中数学 来源: 题型:
【题目】近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
最喜爱的一种活动统计表
活动形式 | 征文 | 讲故事 | 演讲 | 网上竞答 | 其他 |
人数 | 60 | 30 | 39 | a | b |
(1)在这次抽样调查中,一共调查了多少名学生?扇形统计图中“讲故事”部分的圆心角是多少度?
(2)如果这所中学共有学生3800名,那么请你估计最喜爱征文活动的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AB=4cm,C为AB上一动点,过点C的直线交⊙O于D、E两点,且∠ACD=60°,DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时,设AF=xcm,DE=ycm(当x的值为0或3时,y的值为2),探究函数y随自变量x的变化而变化的规律.
(1)通过取点、画图、测量,得到了x与y的几组对应值,如下表:
x/cm | 0 | 0.40 | 0.55 | 1.00 | 1.80 | 2.29 | 2.61 | 3 |
y/cm | 2 | 3.68 | 3.84 | 3.65 | 3.13 | 2.70 | 2 |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:点F与点O重合时,DE长度约为 cm(结果保留一位小数).

查看答案和解析>>
科目:初中数学 来源: 题型:
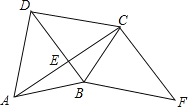
【题目】如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB.
(1)求证:四边形DBFC是平行四边形;
(2)如果BC平分∠DBF,∠F=45°,BD=2,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
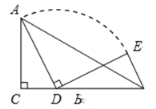
【题目】如图,在△ABC中,∠ACB 90,AC3,CB5,点D是CB边上的一个动点,将线段AD绕着点D 顺时针旋转90,得到线段DE,连结BE,则线段BE的最小值等于__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
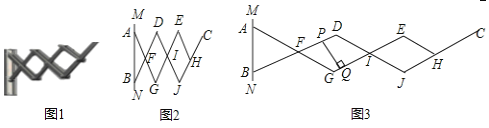
【题目】如图1,是一个三节段式伸缩晾衣架,如图2,是其衣架侧面示意图.MN为衣架的墙体固定端,A为固定支点,B为滑动支点,四边形DFGI和四边形EIJH是菱形,且AF=BF=CH=DF=EH.点B在AN上滑动时,衣架外延钢体发生角度形变,其外延长度(点A和点C间的距离)也随之变化,形成衣架伸缩效果.伸缩衣架为初始状态时,衣架外延长度为42cm.当点B向点A移动8cm时,外延长度为90cm.如图3,当外延长度为120cm时,则BD和GE的间距PQ长为______________cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com