
【题目】已知:点O到△ABC的两边AB、AC所在直线的距离OD=OE,且OB=OC.
(1)如图,若点O在BC上,求证:AB=AC;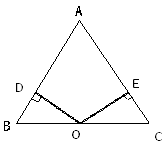
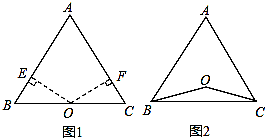
(2)如图,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.
【答案】
(1)解:证明:过点O分别作OE⊥AB于E,OF⊥AC于F,
由题意知,
在Rt△OEB和Rt△OFC中
![]()
∴Rt△OEB≌Rt△OFC(HL), (1)由HL判断出Rt△OEB≌Rt△OFC ,根据全等三角形对应角相等得出∠ABC=∠ACB ,根据等角等等边得出AB=AC ;
∴∠ABC=∠ACB,
∴AB=AC
(2)证明:过点O分别作OD⊥AB于D,OE⊥AC于E,
由题意知,OE=OF.∠BEO=∠CFO=90°,
∵在Rt△OEB和Rt△OFC中
![]()
∴Rt△OEB≌Rt△OFC(HL),
∴∠OBE=∠OCF,
又∵OB=OC,
∴∠OBC=∠OCB,
∴∠ABC=∠ACB,
∴AB=AC;
(3)解:不一定成立,当∠A的平分线所在直线与边BC的垂直平分线重合时AB=AC,否则AB≠AC.(如图)
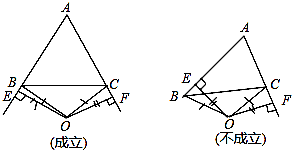
【解析】 (1)由HL判断出Rt△OEB≌Rt△OFC ,根据全等三角形对应角相等得出∠ABC=∠ACB ,根据等角等等边得出AB=AC ;
(2)过点O分别作OD⊥AB于D,EF⊥AC于E,根据HL判断出Rt△ODB≌Rt△OEC ,根据全等三角形的性质得出∠OBD=∠OCE,由根据等边对等角得出∠OBC=∠OCB,从而得出∠ABC=∠ACB,根据等角对等边得出AB=AC;
(3)不一定成立,当∠A的平分线所在直线与边BC的垂直平分线重合时AB=AC,否则AB≠AC.(如图)
【考点精析】通过灵活运用角平分线的性质定理和线段垂直平分线的性质,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方![]() 米处的点C出发,沿斜面坡度
米处的点C出发,沿斜面坡度![]() 的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈
的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() .计算结果保留根号)
.计算结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件为必然事件的是( )
A.打开电视,正在播放新闻B.买一张电影票,座位号是奇数号
C.抛一枚骰子,抛到的数是整数D.掷一枚质地均匀的硬币,正面朝上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为绿化校园,在一块长24米,宽19米的长方形空地的中央建造一个面积为300平方米的长方形花圃,要使四周留出一条宽相等的小路,可设小路宽为x,从而列出方程,求得小路的宽为________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】往一个长25m,宽11m的长方体游泳池注水,水位每小时上升0.32m,
(1)写出游泳池水深d(m)与注水时间x(h)的函数表达式;
(2)如果x(h)共注水y(m3),求y与x的函数表达式;
(3)如果水深1.6m时即可开放使用,那么需往游泳池注水几小时?注水多少(单位:m3)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中有红球、白球共10个,这些球除色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有60次摸到红球.请你估计这个口袋中有_____个白球.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com