
| 1 |
| 4 |
| 9 |
| 4 |
|
|
| 3 |
| 7 |
|
|


科目:初中数学 来源: 题型:
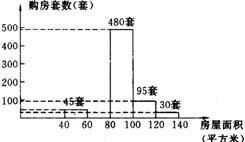 42、随着人民生活水平的提高,购房者对居住面积的要求有了新的变化.现从我区近期卖出的不同户型的商品房中随机抽取1000套进行统计,并根据统计结果绘出如图所示的统计图,请结合统计图提供的信息,解答下列问题:
42、随着人民生活水平的提高,购房者对居住面积的要求有了新的变化.现从我区近期卖出的不同户型的商品房中随机抽取1000套进行统计,并根据统计结果绘出如图所示的统计图,请结合统计图提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
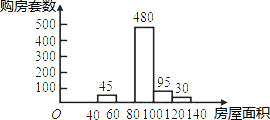 计结果绘出如图所示的统计图,请结合统计图提供的信息,解答下列问题:
计结果绘出如图所示的统计图,请结合统计图提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(湖北黄冈卷)数学(解析版) 题型:选择题
随着人民生活水平的提高,我国拥有汽车的居民家庭也越来越多,下列汽车标志中,是中心对称图形的是
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com