
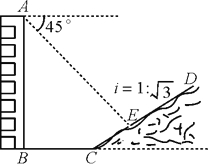
【题目】如图,一楼房AB后有一假山,其坡度为i=1∶![]() ,山坡坡面上E点处有一休息亭,测
,山坡坡面上E点处有一休息亭,测
得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角
为45°,求楼房AB的高.
【答案】(35+10 ![]() )米.
)米.
【解析】试题分析:过点E作EF⊥BC于点F.在Rt△CEF中,求出CF=![]() EF,过点E作EH⊥AB于点H.在Rt△AHE中,∠HAE=45°,得到CF的值,再根据AB=AH+BH,求出AB的值.
EF,过点E作EH⊥AB于点H.在Rt△AHE中,∠HAE=45°,得到CF的值,再根据AB=AH+BH,求出AB的值.
试题解析:过点E作EF⊥BC的延长线于F,EH⊥AB于点H,

在Rt△CEF中,
∵i=![]() =tan∠ECF,
=tan∠ECF,
∴∠ECF=30°,
∴EF=![]() CE=10米,CF=10
CE=10米,CF=10![]() 米,
米,
∴BH=EF=10米,HE=BF=BC+CF=(25+10![]() )米,
)米,
在Rt△AHE中,∵∠HAE=45°,
∴AH=HE=(25+10![]() )米,
)米,
∴AB=AH+HB=(35+10![]() )米.
)米.
答:楼房AB的高为(35+10![]() )米.
)米.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为___________时,△ACP是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 斜边相等的两个直角三角形全等 B. 腰相等的两个等腰三角形全等
C. 有一边相等的等腰直角三角形全等 D. 有一边相等的两个等边三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=x2先向右平移2个单位,再向下平移3个单位,那么所得到抛物线的函数关系式是( )
A.y=(x﹣2)2﹣3
B.y=(x+2)2﹣3
C.y=(x﹣2)2+3
D.y=(x+2)2+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形 ![]() 是正方形,
是正方形, ![]() 是
是 ![]() 垂直平分线上的点,点
垂直平分线上的点,点 ![]() 关于
关于 ![]() 的对称点是
的对称点是 ![]() ,直线
,直线 ![]() 与直线
与直线 ![]() 交于点
交于点 ![]() .
.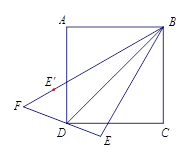
(1)若点 ![]() 是
是 ![]() 边的中点,连接
边的中点,连接 ![]() ,则
,则 ![]() =;
=;
(2)小明从老师那里了解到,只要点 ![]() 不在正方形的中心,则直线
不在正方形的中心,则直线 ![]() 与
与 ![]() 所夹锐角不变.他尝试改变点
所夹锐角不变.他尝试改变点 ![]() 的位置,计算相应角度,验证老师的说法.
的位置,计算相应角度,验证老师的说法.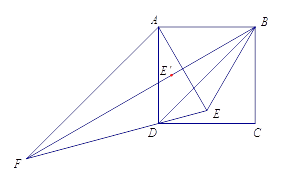
如图,将点 ![]() 选在正方形内,且△
选在正方形内,且△ ![]() 为等边三角形,求出直线
为等边三角形,求出直线 ![]() 与
与 ![]() 所夹锐角的度数;
所夹锐角的度数;
(3)请你继续研究这个问题,可以延续小明的想法,也可用其它方法.
我选择小明的想法;并简述求直线 ![]() 与
与 ![]() 所夹锐角度数的思路.
所夹锐角度数的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求k的值;
(2)点N(a,1)是反比例函数![]() (x>0)图象上的点在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,动点A(a,0)在x轴的正半轴上,定点B(m, n)在第一象限内(m<2≤a).在△OAB外作正方形ABCD和正方形OBEF , 连接FD , 点M为线段FD的中点.作BB1⊥x轴于点B1 , 作FF1⊥x轴于点F1.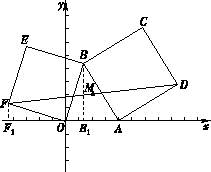
(1)填空:由△≌△ , 及B(m, n)可得点F的坐标为 , 同理可得点D的坐标为;(说明:点F , 点D的坐标用含m , n , a的式子表示)
(2)直接利用(1)的结论解决下列问题:
①当点A在x轴的正半轴上指定范围内运动时,点M总落在一个函数图象上,求该函数的解析式(不必写出自变量x的取值范围);
②当点A在x轴的正半轴上运动且满足2≤a≤8时,求点M所经过的路径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
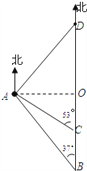
【题目】如图,一艘货船以每小时48海里的速度从港口B出发,沿正北方向航行.在港口B处时,测得灯塔A处在B处的北偏西37°方向上,航行至C处,测得A处在C处的北偏西53°方向上,且A、C之间的距离是45海里.在货船航行的过程中,求货船与灯塔A之间的最短距离及B、C之间的距离;若货船从港口B出发2小时后到达D,求A、D之间的距离.
(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校初一某班学生的平均体重是45公斤.
(1)下表给出了该班6位同学的体重情况(单位:公斤),完成下表
姓 名 | 小丽 | 小华 | 小明 | 小方 | 小颖 | 小宝 |
体 重 | 37 | 50 | 40 |
| 36 | 48 |
体重与平均体重的差值 | ﹣8 | +5 |
| +2 |
|
|
(2)最重的与最轻的同学的体重相差多少?
(3)这6位同学的平均体重是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com