
 如图,若直线y=x被双曲线y=$\frac{{k}^{2}}{x}$与双曲线y=$\frac{2{k}^{2}}{x}$在第一象限截得的线段长为2-$\sqrt{2}$.
如图,若直线y=x被双曲线y=$\frac{{k}^{2}}{x}$与双曲线y=$\frac{2{k}^{2}}{x}$在第一象限截得的线段长为2-$\sqrt{2}$.分析 (1)作AM⊥x轴于M,BN⊥x轴于N,设A点的横坐标为m,B点的横坐标为n,根据题意得出OA=$\sqrt{2}$m,OB=$\sqrt{2}$n,由截得的线段长为2-$\sqrt{2}$,得出$\sqrt{2}$n-$\sqrt{2}$m=2-$\sqrt{2}$,从而求得n-m=$\sqrt{2}$-1,根据m=$\frac{{k}^{2}}{m}$,n=$\frac{2{k}^{2}}{n}$,得出m=k,n=$\sqrt{2}$k,得出$\sqrt{2}$k-k=$\sqrt{2}$-1,解得k=1;
(2)作AD⊥OB,交坐标轴于D,设PE是△PAB边AB上的高,先求得A的坐标,进而求得OA=AD=$\sqrt{2}$,从而求得OD=2,根据三角形的面积求得PE=4+2$\sqrt{2}$,
然后根据AD∥PE,得出$\frac{AD}{PE}$=$\frac{OD}{OP}$,即$\frac{\sqrt{2}}{4+2\sqrt{2}}$=$\frac{2}{OP}$,即可求得P的坐标.
解答 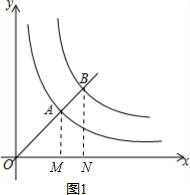 解:(1)如图1,作AM⊥x轴于M,BN⊥x轴于N,设A点的横坐标为m,B点的横坐标为n,
解:(1)如图1,作AM⊥x轴于M,BN⊥x轴于N,设A点的横坐标为m,B点的横坐标为n,
∵A、B是直线y=x上的点,
∴OA=$\sqrt{2}$m,OB=$\sqrt{2}$n,
∵OB-OA=2-$\sqrt{2}$,
∴$\sqrt{2}$n-$\sqrt{2}$m=2-$\sqrt{2}$,
∴$\sqrt{2}$(n-m)=$\sqrt{2}$($\sqrt{2}$-1),
∴n-m=$\sqrt{2}$-1,
∵m=$\frac{{k}^{2}}{m}$,n=$\frac{2{k}^{2}}{n}$,
∴m=k,n=$\sqrt{2}$k,
∴$\sqrt{2}$k-k=$\sqrt{2}$-1,解得k=1;
(2) 存在;
存在;
理由:如图2,作AD⊥OB,交坐标轴于D,设PE是△PAB边AB上的高,
由直线y=x可知OA=AD,
解$\left\{\begin{array}{l}{y=x}\\{y=\frac{1}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,
∴AD=OA=$\sqrt{2}$
∴OD=2,
∵S△ABP=2,AB=2-$\sqrt{2}$,
∴$\frac{1}{2}$AB•PE=2,即(2-$\sqrt{2}$)•PE=4,
解得PE=4+2$\sqrt{2}$,
∵AD⊥OB,PE⊥OB,
AD∥PE
∴$\frac{AD}{PE}$=$\frac{OD}{OP}$,即$\frac{\sqrt{2}}{4+2\sqrt{2}}$=$\frac{2}{OP}$,
解得OP=4$\sqrt{2}$+4.
∴P(4$\sqrt{2}$+4,0)或(0,4$\sqrt{2}$+4).
点评 本题考查了一次函数和反比例函数的交点问题,一次函数图象上点的坐标特征,反比例函数图象上点的坐标特征,交点坐标以及三角形面积等,借助等腰直角三角形解题是关键.


科目:初中数学 来源: 题型:解答题
 甲、乙两车同时从A、B两地相向而行,设两车行驶的时间为x(h),与A地的距离为y(km),y(km)与x(h)关系如图所示:
甲、乙两车同时从A、B两地相向而行,设两车行驶的时间为x(h),与A地的距离为y(km),y(km)与x(h)关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,是一个半圆和抛物线的一部分围成的“芒果”,已知点A、B、C、D分别是“芒果”与坐标轴的交点,AB是半圆的直径,抛物线的解析式为y=$\frac{3}{2}$x2-$\frac{3}{2}$,则图中CD的长为$\frac{5}{2}$.
如图,是一个半圆和抛物线的一部分围成的“芒果”,已知点A、B、C、D分别是“芒果”与坐标轴的交点,AB是半圆的直径,抛物线的解析式为y=$\frac{3}{2}$x2-$\frac{3}{2}$,则图中CD的长为$\frac{5}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
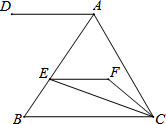 如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=3∠BCF,∠ACF=20°.
如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=3∠BCF,∠ACF=20°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com