
【题目】图(1)是我们常见的“箭头图”,其中隐藏着哪些数学知识呢?下面请你解决以下问题:
(1)观察如图(1)“箭头图”,试探究∠BDC与∠A、∠B、∠C之间大小的关系,并说明理由;
(2)请你直接利用以上结论,回答下列两个问题:
①如图(2),把一块三角板XYZ放置在△ABC上,使其两条直角边XY、XZ恰好经过点B、C.若∠A=50°,求∠ABX+∠ACX
②如图(3),∠ABD,∠ACD的五等分线分别相交于点G1、G2、G3、G4 , 若∠BDC=135°,∠BG1C=67°,求∠A的度数.
【答案】
(1)解:∠BDC=∠A+∠B+∠C.理由:
连接AD并延长到M.

因为∠BDM=∠BAD+∠B,∠CDM=∠CAD+∠C,
所以∠BDM+∠CDM=∠BAD+∠B+∠CAD+∠C,
即∠BDC=∠BAC+∠B+∠C.
(2)解:①由(1)知:∠BXC=∠A+∠ABX+∠ACX,
由于∠BXC=90°,∠A=50°
所以∠ABX+∠ACX
=∠BXC﹣∠A
=90°﹣50°
=40°.
②在箭头图G1BDC中
因为∠BDC=∠G1+∠G1BD+∠G1CD,
又∵∠BDC=135°,∠BG1C=67°
∵∠ABD,∠ACD的五等分线分别相交于点G1、G2、G3、G4
∴4(∠DBG4+∠DCG4)=135°﹣67°
∴∠DBG4+∠DCG4=17°.
∴∠ABG1+∠ACG1=17°
∵在箭头图G1BAC中
∵∠BG1C=∠A+∠G1BA+∠G1CA,
又∵∠BG1C=67°,
∴∠A=50°.
答:∠A的度数是50°.
【解析】第1小题,连接AD并延长到M,利用三角形的一个外角等于和它不相邻的两个内角的和可得∠BDC=∠BAC+∠B+∠C;第2小题,由(1)知:∠BXC=∠A+∠ABX+∠ACX,再根据已知条件可求解。


科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DE , DF分别是△ABD和△ACD的高,连接EF交AD于G.下列结论:①AD垂直平分EF;②EF垂直平分AD;③AD平分∠EDF;④当∠BAC为60°时,AG=3DG , 其中不正确的结论的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“汉字听写大赛”活动,为了解学生的参与情况,在该校随机抽取了四个班级学生进行调查,将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图,请根据图中的信息,解答下列问题:
(1)这四个班参与大赛的学生共__________人;
(2)请你补全两幅统计图;
(3)求图1中甲班所对应的扇形圆心角的度数;
(4)若四个班级的学生总数是160人,全校共2000人,请你估计全校的学生中参与这次活动的大约有多少人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架长25米的梯子,斜靠在竖直的墙上,这时梯子底端离墙7米.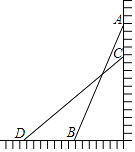
(1)此时梯子顶端离地面多少米?
(2)若梯子顶端下滑4米,那么梯子底端将向左滑动多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别标有数字﹣3,1,3的不透明卡片,它们除数字外都相同,现将它们背面朝上,洗匀后从三张卡片中随机地抽取一张,放回卡片洗匀后,再从三张卡片中随机地抽取一张.
(1)试用列表或画树状图的方法,求两次抽取的卡片上的数字之积为负数的概率;
(2)求两次抽取的卡片上的数字之和为非负数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
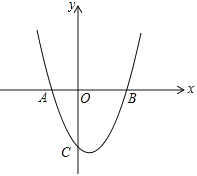
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与x轴交于A(﹣1,0),B(2,0)两点,与y轴交于点C.
与x轴交于A(﹣1,0),B(2,0)两点,与y轴交于点C.
(1)求该抛物线的解析式;
(2)直线y=﹣x+n与该抛物线在第四象限内交于点D,与线段BC交于点E,与x轴交于点F,且BE=4EC.
①求n的值;
②连接AC,CD,线段AC与线段DF交于点G,△AGF与△CGD是否全等?请说明理由;
(3)直线y=m(m>0)与该抛物线的交点为M,N(点M在点N的左侧),点 M关于y轴的对称点为点M',点H的坐标为(1,0).若四边形OM'NH的面积为![]() .求点H到OM'的距离d的值.
.求点H到OM'的距离d的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF. 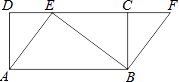
(1)求证:四边形ABFE是平行四边形;
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com