练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．已知四边形ABCD是平行四边形，且A（-2，0），B（1，2），C（3，-2），则D的坐标是（0，-4）．

    分析 设点D的坐标为（x，y），利用平行四边形的对边平行且相等，即可得到3-x=1-（-2），-2-y=2，进而得到D的坐标．

    解答 解：设点D的坐标为（x，y），
    ∵四边形ABCD是平行四边形，且A（-2，0），B（1，2），C（3，-2），
    ∴3-x=1-（-2），-2-y=2，
    解得x=0，y=-4，
    ∴点D的坐标为（0，-4），

    故答案为：（0，-4）．

    点评 本题考查了平行四边形的性质以及坐标与图形性质，熟练掌握平行四边形的性质是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．（1）解不等式2（2-x）≤6-（3x-2）；
    （2）解不等式组$\left\{\begin{array}{l}\frac{3x-1}{5}-\frac{2x+1}{2}≤1\\ 7x-2＜5x+4.\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

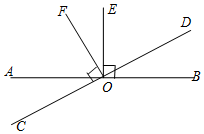    19．如图，直线AB与CD相交于点O，OE⊥AB，OF⊥CD．
    （1）图中∠AOF的余角是∠AOC，∠EOF，∠BOD（把符合条件的角都填出来）．
    （2）图中除直角相等外，还有相等的角，请写出三对：
    ①∠AOC=∠EOF；②∠AOF=∠EOD；③∠EOC=∠BOF．
    （3）如果∠EOF=$\frac{1}{5}$∠AOD，求∠EOF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．计算：5$\sqrt{\frac{1}{5}}$-$\frac{5}{4}$$\sqrt{\frac{4}{5}}$+$\sqrt{45}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．解不等式组：$\left\{\begin{array}{l}{3（x-2）≥x-4}\\{\frac{2x+1}{3}＞x-1}\end{array}\right.$，并把解集在数轴上表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

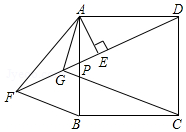    13．如图，正方形ABCD中，P为AB边上任意一点，AE⊥DP于E，点F在DP的延长线上，且EF=DE，连接AF、BF，∠BAF的平分线交DF于G，连接GC．
    （1）求证：△AEG是等腰直角三角形；
    （2）求证：AG+CG=$\sqrt{2}$DG．

    查看答案和解析>>

    科目：初中数学 来源：2017届山东泰安市中考二模数学试卷（解析版） 题型：解答题

    在平面直角坐标系xOy中，抛物线y=mx2﹣2mx﹣3（m≠0）与x轴交于A（3，0），B两点．

    （1）求抛物线的表达式及点B的坐标；

    （2）当﹣2＜x＜3时的函数图象记为G，求此时函数y的取值范围；

    （3）在（2）的条件下，将图象G在x轴上方的部分沿x轴翻折，图象G的其余部分保持不变，得到一个新图象M．若经过点C（4.2）的直线y=kx+b（k≠0）与图象M在第三象限内有两个公共点，结合图象求b的取值范围．

    查看答案和解析>>

    科目：初中数学 来源：2017届山东泰安市中考二模数学试卷（解析版） 题型：单选题

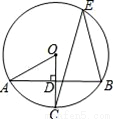
    如图，A，B，E为⊙0上的点，⊙O的半径OC⊥AB于点D，若∠CEB=30°，OD=1，则AB的长为（　　）

    A. 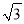B. 4 C. 2 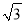D. 6

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．下列运算正确的是（　　）
    A．a3•a3=2a3B．a3+a3=2a6C．a6÷a3=a2D．（-2a2）3=-8a6

    查看答案和解析>>

    同步练习册答案