
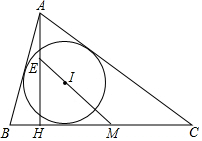
 在△ABC中,M是BC边的中点,I是内切圆的圆心,AH⊥BC于点H,E是直线IM与AH的交点,求证:AE=r.其中r是内切圆的半径.
在△ABC中,M是BC边的中点,I是内切圆的圆心,AH⊥BC于点H,E是直线IM与AH的交点,求证:AE=r.其中r是内切圆的半径. 分析 设圆I与BC相切于P,连接IP,设AB=c,AC=b,BC=a,根据已知条件得到BM=$\frac{a}{2}$,根据切线的性质得到PB=$\frac{a+c-b}{2}$,根据三角函数的定义得到BH=c•cos∠B=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2a}$,根据相似三角形的性质得到EH=r•$\frac{b+c}{a}$①
根据三角形的面积公式得到AH=$\frac{a+b+c}{a}$•r②,于是得到结论.
解答 证明: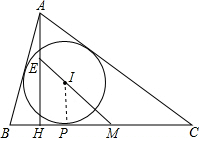 设圆I与BC相切于P,连接IP,
设圆I与BC相切于P,连接IP,
设AB=c,AC=b,BC=a,
则BM=$\frac{a}{2}$,PB=$\frac{a+c-b}{2}$,BH=c•cos∠B=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2a}$,
∵△IPM∽△MEH,
∴$\frac{IH}{IP}$=$\frac{HM}{PM}$=$\frac{BM-BH}{BM-BP}$=$\frac{\frac{{a}^{2}}{2}-\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2a}}{\frac{a}{2}-\frac{a+c-b}{2}}$=$\frac{b+c}{a}$,
∴EH=r•$\frac{b+c}{a}$①
三角形的面积公式知a•AH=(a+b+c),
∴AH=$\frac{a+b+c}{a}$•r②,
结合①,②可得AE=AH-EH=$\frac{a+b+c}{a}$•r-r•$\frac{b+c}{a}$=r
点评 本题考查了三角形的内切圆与内心,相似三角形的判定和性质,解直角三角形,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
| 医疗费用 | 门诊 | 住院 | ||
| 0-4000元 | 4001-20000元 | 20000以上 | ||
| 每年报销比例标准 | 40% | 40% | a% | 60% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
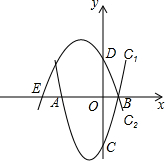 已知抛物线C1:y=x2+2x-3与x轴交于点A,B(点A在点B左侧),与y轴交于点C,抛物线C2:y=ax2+bx+c经过点B,与x轴的另一个交点为E(-4,0),与y轴交于点D(0,2).
已知抛物线C1:y=x2+2x-3与x轴交于点A,B(点A在点B左侧),与y轴交于点C,抛物线C2:y=ax2+bx+c经过点B,与x轴的另一个交点为E(-4,0),与y轴交于点D(0,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
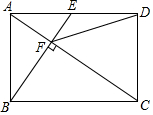 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;正确的是( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;正确的是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
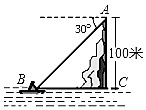 如图,在高出海平面100m的悬崖顶A处,观测海面上的一艘小船B,并测得它的俯角为30°,则船与观测者之间的水平距离为( )
如图,在高出海平面100m的悬崖顶A处,观测海面上的一艘小船B,并测得它的俯角为30°,则船与观测者之间的水平距离为( )| A. | 50$\sqrt{3}$ | B. | 100 | C. | 100+$\sqrt{3}$ | D. | 100$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com