
【题目】如图,一块铁片边缘是由抛物线和线段AB组成,测得AB=20cm,抛物线的顶点到AB边的距离为25cm.现要沿AB边向上依次截取宽度均为4cm的矩形铁皮,从下往上依次是第一块,第二块…如图所示.已知截得的铁皮中有一块是正方形,则这块正方形铁皮是第块. 
【答案】6
【解析】解:如图,建立平面直角坐标系.
∵AB=20cm,抛物线的顶点到AB边的距离为25cm,
∴此抛物线的顶点坐标为:(10,25),图象与x轴的交点坐标为:(0,0),(20,0),
∴抛物线的解析式为:y=a(x﹣10)2+25,
解得:0=100a+25,
a=﹣ ![]() ,
,
∴y=﹣ ![]() (x﹣10)2+25,
(x﹣10)2+25,
现要沿AB边向上依次截取宽度均为4cm的矩形铁皮,
∴截得的铁皮中有一块是正方形时,正方形边长一定是4cm.
∴当四边形DEFM是正方形时,DE=EF=MF=DM=4cm,
∴M点的横坐标为AN﹣MK=10﹣2=8,
即x=8,代入y=﹣ ![]() (x﹣10)2+25,
(x﹣10)2+25,
解得:y=24,
∴KN=24,24÷4=6,
∴这块正方形铁皮是第六块,
所以答案是:6.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′,记旋转角为α.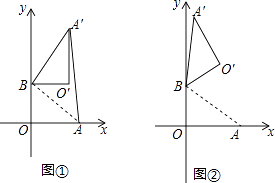
(1)如图①,若α=90°,求AA′的长;
(2)如图②,若α=120°,求点O′的坐标;
(3)在(Ⅱ)的条件下,边OA上 的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,求点P′的坐标(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y1=﹣ ![]() x﹣1与反比例函数y2=
x﹣1与反比例函数y2= ![]() 的图象交于点A(﹣4,m).
的图象交于点A(﹣4,m). 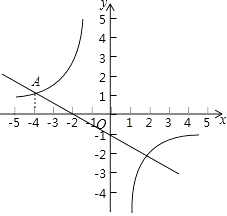
(1)观察图象,在y轴的左侧,当y1>y2时,请直接写出x的取值范围;
(2)求出反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(2,2),B(4,1),C(4,4).
(1)作出 ![]() ABC关于原点O成中心对称的
ABC关于原点O成中心对称的 ![]() A1B1C1.
A1B1C1.
(2)作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在 ![]() A1B1C1的内部(不包括顶点和边界),求a的取值范围.
A1B1C1的内部(不包括顶点和边界),求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H;下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=∠BAC-∠C;④∠BGH=∠ABE+∠C,其中正确的结论有___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数;
(3)如图③,若把“AE⊥BC”变成“AE平分∠BEC”,其它条件不变,∠DAE的大小是否变化,并请说明理由.
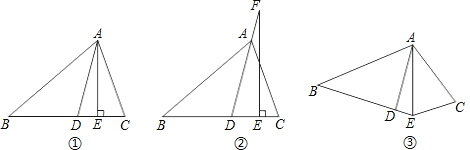
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=kx+b交x轴于点A,交y轴于点B,直线y=2x﹣4交x轴于点D,与直线AB相交于点C(3,2).
(1)根据图象,写出关于x的不等式2x﹣4>x+b的解集;
(2)若点A的坐标为(5,0),求直线AB的解析式;
(3)在(2)的条件下,求四边形BODC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次考试中,某班级的数学成绩统计图如下.下列说法错误的是( )

A. 得分在70~80分之间的人数最多
B. 该班的总人数为40
C. 得分在90~100分之间的人数最少
D. 及格(≥60分)人数是26
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com