Question

已知A（-1，0），B（0，-3），点C与点A关于坐标原点对称，经过点C的直线与y轴交于点D，与直线AB交于点E，且E点在第二象限．
（1）求直线AB的解析式；
（2）若点D（0，1），过点B作BF⊥CD于F，连接BC，求∠DBF的度数及△BCE的面积；
（3）若点G（G不与C重合）是动直线CD上一点，且BG=BA，试探究∠ABG与∠ACE之间满足的等量关系，并加以证明．

Answer 1

分析：（1）设直线AB的解析式为y=kx-3，将点A（-1，0）代入求得k值即可求得函数的解析式；
（2）根据点C的坐标求得OC=1．由D（0，1），得OD=1．求得直线CD的解析式为y=-x+1然后与直线y=3x-3联立即可求得两直线的交点E的坐标，过E作EH⊥y轴于H，则EH=2．再根据B、D的坐标求得BD=4．然后利用S_△BCE=S_△BDE+S_△BDC即可求得三角形BCE的面积．
（3）连接BC，作BM⊥CD于M．设∠CBO=α，则∠ABO=α，∠ACB=90°-α，∠CBM=β，则∠GBM=β，∠BCG=90°-β．然后分当点G在射线CD的反向延长线上时和当点G在射线CD的延长线上时两种情况讨论即可得到答案．

解答：解：（1）依题意，设直线AB的解析式为
y=kx-3
∵A（-1，0）在直线上，
∴0=-k-3．
∴k=-3．
∴直线AB的解析式为y=-3x-3．…（1分）

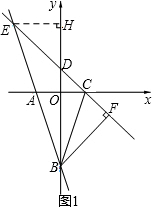
（2）如图1，依题意，C（1，0），OC=1．
由D（0，1），得OD=1．
在△DOC中，∠DOC=90°，OD=OC=1．
可得∠CDO=45°．
∵BF⊥CD于F，
∴∠BFD=90°．
∴∠DBF=90°-∠CDO=45°．…（2分）
可求得直线CD的解析式为y=-x+1
由 

y=-3x-3 y=-x+1

 解得

x=-2 y=3

∴直线AB与CD的交点为E（-2，3）．…（3分）
过E作EH⊥y轴于H，则EH=2．
∵B（0，-3），D（0，1），
∴BD=4．
∴S_△BCE=S_△BDE+S_△BDC=

1

2

×4×2+

1

2

×4×1=6…（4分）

（3）连接BC，作BM⊥CD于M．
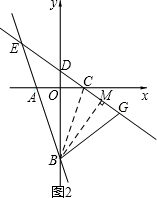
∵AO=OC，BO⊥AC，
∴BA=BC．
∴∠ABO=∠CBO．
设∠CBO=α，则∠ABO=α，∠ACB=90°-α．
∵BG=BA，
∴BG=BC．
∵BM⊥CD，
∴∠CBM=∠GBM．
设∠CBM=β，则∠GBM=β，∠BCG=90°-β．
（i） 如图2，当点G在射线CD的反向延长线上时，
∵∠ABG=2α+2β=2（α+β）
∠ECA=180°-（90°-α）-（90°-β）=α+β
∴∠ABG=2∠ECA．…（6分）
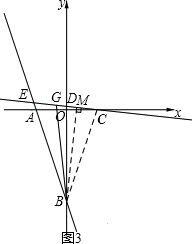
（ii） 如图3，当点G在射线CD的延长线上时，
∵∠ABG=2α-2β=2（α-β）
∠ECA=（90°-β）-（90°-α）=α-β
∴∠ABG=2∠ECA．…（7分）
综上，∠ABG=2∠ECA．
说明：第（3）问两种情况只要做对一种给 （2分）；累计（3分）．

点评：本题考查了一次函数的综合知识，题目中渗透了分类讨论的数学思想，题目难度较大．