
 如图,某生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动12米到B处,测得∠EBF=30°,∠CBD=45°,sin∠CAD=$\frac{3}{5}$.
如图,某生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动12米到B处,测得∠EBF=30°,∠CBD=45°,sin∠CAD=$\frac{3}{5}$.分析 (1)汽车∠BEA=30°=∠EBF,得出AB=AE=12米,在△AEF中,由三角函数汽车EF即可;
(2)设CD=x米,证出BD=CD=x米,由三角函数得出方程,解方程求出x,再求出AF,即可得出结果.
解答 解:(1)∵∠EAF=60°,∠EBF=30°,
∴∠BEA=30°=∠EBF,
∴AB=AE=12米,
在△AEF中,EF=AE×sin∠EAF=12×sin60°=6$\sqrt{3}$米,
答:旗杆EF的高为6$\sqrt{3}$米;
(2)设CD=x米,
∵∠CBD=45°,∠D=90°,
∴BD=CD=x米,
∵sin∠CAD=$\frac{3}{5}$,
∴tan∠CAD=$\frac{CD}{AD}$=$\frac{3}{4}$,
∴$\frac{x}{x+12}=\frac{3}{4}$,
解得:x=36米,
在△AEF中,∠AEF=60°-30°=30°,
∴AF=$\frac{1}{2}$AE=6米,
∴DF=BD+AB+AF=36+12+6=54(米),
答:旗杆EF与实验楼CD之间的水平距离DF的长为54米.
点评 本题考查了解直角三角形的应用、等腰三角形的判定、等腰直角三角形的判定与性质;熟练掌握解直角三角形,由三角函数得出方程是解决问题的关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题
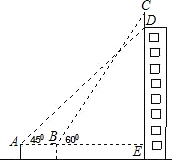 如图某幢大楼顶部有一广告牌CD,甲、乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°和60°,且A、B、E三点在一直线(∠AEC=90°)上,若BE=15米,求这块广告牌的CD.(取 $\sqrt{3}$=1.73,计算结果保留整数)
如图某幢大楼顶部有一广告牌CD,甲、乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°和60°,且A、B、E三点在一直线(∠AEC=90°)上,若BE=15米,求这块广告牌的CD.(取 $\sqrt{3}$=1.73,计算结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 用笔数(支) | 4 | 5 | 6 | 8 | 8 |
| 学生数 | 4 | 4 | 7 | 3 | 2 |
| A. | 众数是7支 | B. | 中位数是6支 | C. | 平均数是5支 | D. | 方差为0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知,在平面直角坐标系中,A(-3,-4),B(0,-2).
如图,已知,在平面直角坐标系中,A(-3,-4),B(0,-2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com