
����Ŀ�����һ�����м���취������취�������ÿ��취�����ж��ֲ�ͬ�İ취�����������µIJ�ͬ�취���Ǹ��ͬ���������ĺͣ�����Ƿ������ԭ����Ҳ�����ӷ�ԭ�������һ���£���Ҫ�ֳɼ������裬ÿһ��������ж��ֲ�ͬ�ķ��������������µIJ�ͬ���������Ǹ��ֲ�ͬ�ķ������ij˻�������Ƿֲ�����ԭ����Ҳ�����˷�ԭ����
С��ͬѧ�μ�ij����ѧУ���е������������ԣ����ο��Թ���1000�˲μӣ�
��1��1000�˲μ����п��ԣ���300�˿������ܼӷ����ߣ�����10��20��30��60�ĸ����Σ�С����������30�ֵļӷ֣���ô����Ϊ���٣�
��2�����ø��е��п�¼ȡ������Ϊ530�֣�С�������п�����������500-509��510-519��520-529�����ֶΣ�
����С�����п�������510~519�ֶΣ���С�����ø���¼ȡ�ĸ���Ϊ���٣�
����С�����п����������������ζ�Ӧ�ĸ��ʷֱ�Ϊ![]() ��
��![]() ��
��![]() ����С�����ø���¼ȡ�ĸ���Ϊ���٣�
����С�����ø���¼ȡ�ĸ���Ϊ���٣�
�ӷ� | ���� |
10 | 30 |
20 | 90 |
30 | 150 |
60 | 30 |
���𰸡���1��![]() ����2����
����2����![]() ����
����![]() ��
��
��������
��1��1000�˲μ����п��ԣ��������30�ֵļӷֵ�������180�ˣ��ɴ������С���������30�ֵļӷֵĸ��ʣ�
��2����С�����ø���¼ȡ����Ҫ�������20�ֵļӷ֣��ɴ������С�����ø���¼ȡ�ĸ��ʣ����ȷֱ�ó�С���������10�֣�20�֣�30�ֵļӷָ��ʣ��������Ķ�����������ʵij˷�ԭ���ͼӷ�ԭ���������С�����ø���¼ȡ�ĸ��ʣ�
�⣺��1����1000�˲μ����п��ԣ��������30�ֵļӷֵ������У�150+30=180���ˣ���
��С���������30�ֵļӷֵĸ���Ϊ��![]() ��
��
��2���١�С�����п�������510~519�ֶΣ����ø��е��п�¼ȡ������Ϊ530�֣�
��С�����ø���¼ȡ����Ҫ�������20�ֵļӷ֣�
��С�����ø���¼ȡ�ĸ���Ϊ��![]() ��
��
�ڡ߸ø��е��п�¼ȡ������Ϊ530�֣�С�������п�����������500-509��510-519��520-529�����ֶΣ������������ζ�Ӧ�ĸ��ʷֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��
��С���������10�ֵļӷָ���Ϊ��![]() ���������20�ֵļӷָ���Ϊ��
���������20�ֵļӷָ���Ϊ��![]() ���������30�ֵļӷָ���Ϊ��
���������30�ֵļӷָ���Ϊ��![]() ��
��
��С�����ø���¼ȡ�ĸ���Ϊ��![]() ��
��![]() +
+![]() ��
��![]() +
+![]() ��
��![]() =
=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
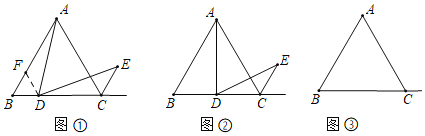
����Ŀ��һ����ѧ�κ���ʦ������һ���κ���ϰ����ABC�ǵȱ������Σ���D���߶�BC�ϵĵ㣬��EΪ��ABC�����ƽ������һ�㣬�ҡ�ADE��60������ͼ�٣�����D���߶�BC�ϣ���B��C�⣩����һ��ʱ����֤��AD��DE
��1������˼·����ɽ��
����֤��˼·���������п�ͼ����

��������˼·��������������д�����֤�����̣�
��2������λ�ã��������
����DΪBC���е�ʱ���ȱߡ�ABC�ı߳�Ϊ6�����DE�ij���
��3��֪ʶǨ�ƣ�̽����֪
����D���߶�BC���ӳ����ϣ�������CD��BCʱ����AB��2����ֱ��д����ADE�����������д�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��չУ��������������ѡ�������������Ϊ����������ǿ����������Т�ϰ�����������ʵ�������������ÿλͬѧֻ�ܲ�������һ�࣬��ѡ��������ѡ��20λУ����������������ͳ�ƣ�����������ͳ�Ʊ����������֣�ͳ�Ʊ���ǰ���е����ݶ�����ȷ�ģ������е���������һ���Ǵ���ģ�
��� | Ƶ�� | Ƶ�� |
�������������� | a | 0.20 |
��ǿ������������ | 3 | b |
Т�ϰ����������� | 7 | 0.35 |
��ʵ������������ | 6 | 0.32 |
����������Ϣ������������⣺
��1��ͳ�Ʊ��е�a���� ����b�� ����
��2��ͳ�Ʊ������д������������ ���������ݵ���ȷֵ���� ����
��3��УС���߾�����A��B��C��λ����ǿ��������������������ɷ���λ���û���״ͼ���б��ķ�������A��B�����ɷõ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P1OA1����P2A1A2����P3A2A3�������ǵ���ֱ�������Σ���P1��P2��P3�������ڷ���������y��![]() ��ͼ���ϣ�б��OA1��A1A2��A2A3��������x���ϣ����A3��������_____��
��ͼ���ϣ�б��OA1��A1A2��A2A3��������x���ϣ����A3��������_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���ʵؾ��ȵ�����������ĸ��������α�������-2��0��1��2�������������Σ�����һ������ֱַ���a��b��������ΪM��ĺᡢ�����꣬���M(a��b)������A(6��0)��B(2��0)��C(0��2)Ϊ�������������(�����߽�)�ĸ�����________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��B������ֱ�Ϊ����2��3���ͣ�1��3����������y=ax2+bx+c��a��0���� �������߶�AB���˶�ʱ����״���ֲ��䣬����x�ύ��C��D���㣨C��D����ࣩ���������н��ۣ���c��3���ڵ�x����3ʱ��y��x���������������D�ĺ��������ֵΪ5�����C�ĺ�������СֵΪ��5���ܵ��ı���ACDBΪƽ���ı���ʱ��a��![]() ��������ȷ���ǣ� ��
��������ȷ���ǣ� ��
A. �ڢ� B. �ڢ� C. �٢ۢ� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��֪A(3��0),B(0��-1)������AB,��B����AB�Ĵ��߶�,ʹBA=BC,����AC.
(1)��ͼ1����C�����ꣻ
(2)��ͼ2,��P���A�����,��x������ƽ��,����BP,������ֱ����������BPQ,����CQ.��֤:PA=CQ.
(3)��(2)��������,��C��P��Q���㹲��,���ʱP�����꼰��APB�Ķ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��l��y��x+b��x�ύ�ڵ�A����2��0������y�ύ�ڵ�B��˫����y![]() ��ֱ��l����P��Q���㣬���е�P����������ڵ�Q��������
��ֱ��l����P��Q���㣬���е�P����������ڵ�Q��������
��1�����B�����ꣻ
��2������P�ĺ�����Ϊ2ʱ����k��ֵ��
��3������PO������POB�����ΪS����![]() ����Ϻ���ͼ��ֱ��д��k��ȡֵ��Χ��
����Ϻ���ͼ��ֱ��д��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���ƶ�ȫ����Ծ���ѧ���ط��÷����ٽ�ȫ�������ι���ij��ÿ�궼�ٰ��շ�֪ʶ����������ij��λ�ס����������Ÿ���Ա��200�ˣ�Ҫ����������������ѡһ�����Ŵ�����λ�μӽ���ľ�����Ϊ�˽�����������Ա���Է���֪ʶ����������������˳������飬�Ӽס����������Ÿ������ȡ20��Ա���������˷���֪ʶ���ԣ���������ǵijɼ����ٷ��ƣ����������ݣ��ɼ������������������ͷ�������������˲�����Ϣ��
a���ײ��ųɼ���Ƶ���ֲ�ֱ��ͼ���£����ݷֳ�6�飺40��x��50��50��x��60��60��x��70��70��x��80��80��x��90��90��x��100��
b���Ҳ��ųɼ����£�
40 52 70 70 71 73 77 78 80 81
82 82 82 82 83 83 83 86 91 94
c���ס��������ųɼ���ƽ�����������λ�����£�
ƽ���� | ���� | ��λ�� | |
�� | 79.6 | 36.84 | 78.5 |
�� | 77 | 147.2 | m |
d��������õ�λ����Ա�����븴���ij��߳ɼ����£�
2014�� | 2015�� | 2016�� | 2017�� | 2018�� | |
���߳ɼ����ٷ��ƣ� | 79 | 81 | 80 | 81 | 82 |
����������Ϣ���ش��������⣺
��1��д������m��ֵ��
��2�������ƶϳ�ѡ���� �����Ų������ã�����Ϊ�� ����
��3��Ԥ����2���в��Ž���������븴��������Ϊ�� ����

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com