
解:(1)过A作AH⊥BC于H,
∵AB=AC=5,BC=6,
∴BH=

BC=3,
∴AH=

=

=4,
∴S
△ABC=

BC•AH=

×6×4=12.
(2)令此时正方形的边长为a,
∵DE∥BC,
∴

,

∴a=

.
(3)当DE=

时,由△ADE∽△ABC得

=

,解得AD=2,
当0<x≤2时,正方形全部在三角形内部,由

=

得:

=

,DE=

x,
y=(

x)
2=
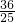
x
2,
当2<x<5时,y=
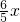
•

(5-x)=

x-

x
2.
(4)当△BDG是等腰三角形时,设AD=x,当BD=DG,
此时正方形不全部在三角形内部,
∵BD=5-x,
由(3)可知DG=DE=

x,
由此即可求出AD=

;
当DB=BG时,求出AD=

;
当DG=BG,求出AD=

;
故
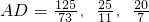
.
分析:(1)作底边上的高,利用勾股定理求出高就可以求出面积.
(2)根据DE∥BC,得到△ADE∽△ABC,再根据相似三角形对应高的比等于相似比即可求出边DE的长度.
(3)可以分为正方形在三角形内部和不全在内部两种情况求解,全在内部时,利用三角形相似得

=

,求出DE,再求重叠部分正方形的面积,不全在内部时先求出长DE,再利用DG∥AH,求出宽.
(4)当△BDG是等腰三角形时,分BD=DG,BD=BG,DG=BG三种情况写出AD的长.
点评:本题考查了正方形、等腰三角形的性质,相似比等相关知识,解题时,注意形数结合,分类讨论.

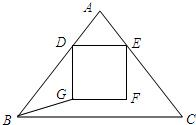 重合),且保持DE∥BC,以DE为边,在点A的异侧作正方形DEFG.
重合),且保持DE∥BC,以DE为边,在点A的异侧作正方形DEFG. 解:(1)过A作AH⊥BC于H,
解:(1)过A作AH⊥BC于H, BC=3,
BC=3, =
= =4,
=4, BC•AH=
BC•AH= ×6×4=12.
×6×4=12. ,
,
 .
. 时,由△ADE∽△ABC得
时,由△ADE∽△ABC得 =
= ,解得AD=2,
,解得AD=2, =
= 得:
得: =
= ,DE=
,DE= x,
x, x)2=
x)2=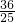 x2,
x2,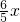 •
• (5-x)=
(5-x)= x-
x- x2.
x2. x,
x, ;
; ;
; ;
;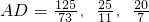 .
. =
= ,求出DE,再求重叠部分正方形的面积,不全在内部时先求出长DE,再利用DG∥AH,求出宽.
,求出DE,再求重叠部分正方形的面积,不全在内部时先求出长DE,再利用DG∥AH,求出宽.

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为