【题目】如图的
中，
，且
为
上一点．今打算在
上找一点
，在
上找一点
，使得
与
全等，以下是甲、乙两人的作法：
（甲）连接
，作的中垂线分别交、于点、点，则、两点即为所求
（乙）过作与平行的直线交于点，过作与平行的直线交于点，则、两点即为所求
对于甲、乙两人的作法，下列判断何者正确？（ ）
A. 两人皆正确B. 两人皆错误
C. 甲正确，乙错误D. 甲错误，乙正确
53随堂测系列答案科目：初中数学 来源： 题型：
【题目】如图，在正方形ABCD中，E、F分别是边AD、CD上的点，AE=ED，DF=
DC，连接EF并延长交BC的延长线于点G．
（1）求证：△ABE∽△DEF；
（2）若正方形的边长为4，求BG的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个分数（分子、分母均为正整数）的分母比它的分子大5．
（1）若将这个分数的分子加上14，分母减去1，则所得的分数是原分数的倒数，求这个分数；
（2）若将这个分数的分子、分母同时加上4，试比较所得的分数和原分数的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点O是等腰直角三角形ABC斜边上的中点，AB=BC,E是AC上一点，连结EB.
(1) 如图1，若点E在线段AC上,过点A作AM⊥BE，垂足为M，交BO于点F．求证：OE=OF；
(2)如图2，若点E在AC的延长线上，AM⊥BE于点M，交OB的延长线于点F，其它条件不变，则结论“OE=OF”还成立吗？如果成立，请给出证明；如果不成立，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,AD是Rt△ABC斜边BC上的高.
（1）尺规作图:作∠C的平分线,交AB于点E,交AD于点F（不写作法,必须保留作图痕迹,标上应有的字母）;
（2）在（1）的条件下,过F画BC的平行线交AC于点H,线段FH与线段CH的数量关系如何?请予以证明;
（3）在（2）的条件下,连结DEDH.求证:ED⊥HD.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，两边PE、PF分别交AB、AC于点E、F，给出下列四个结论：
①AE=CF；
②△EPF是等腰直角三角形；
③EF=AB；
④
，当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合)，上述结论中始终正确的有________(把你认为正确的结论的序号都填上).
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们知道，各个角都相等，各条边都相等的多边形叫做正多边形．对一个各条边都相等的凸多边形（边数大于3），可以由若干条对角线相等判定它是正多边形．例如，各条边都相等的凸四边形，若两条对角线相等，则这个四边形是正方形．
（1）已知凸五边形
的各条边都相等．
①如图1，若
，求证：五边形是正五边形；
②如图2，若
，请判断五边形是不是正五边形，并说明理由：
（2）判断下列命题的真假．（在括号内填写“真”或“假”）
如图3，已知凸六边形
的各条边都相等．
①若
，则六边形是正六边形；（ ）
②若
，则六边形是正六边形． （ ）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC是等边三角形，△ABD是等腰直角三角形，∠BAD=90°，AE⊥BD于点E，连CD分别交AE，AB于点F，G，过点A作AH⊥CD交BD于点H．则下列结论：①∠ADC=15°；②AF=AG；③AH=DF；④△AFG∽△CBG；⑤AF=（
﹣1）EF．其中正确结论的个数为（ ）
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，某日的钱塘江观潮信息如表：
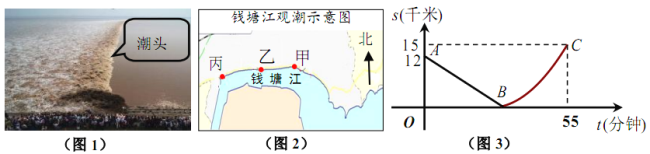
按上述信息，小红将“交叉潮”形成后潮头与乙地之间的距离
（千米）与时间
（分钟）的函数关系用图3表示，其中：“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点
，点
坐标为
，曲线
可用二次函数
（
，
是常数）刻画．
（1）求
的值，并求出潮头从甲地到乙地的速度；
（2）11:59时，小红骑单车从乙地出发，沿江边公路以
千米/分的速度往甲地方向去看潮，问她几分钟后与潮头相遇？
（3）相遇后，小红立即调转车头，沿江边公路按潮头速度与潮头并行，但潮头过乙地后均匀加速，而单车最高速度为
千米/分，小红逐渐落后，问小红与潮头相遇到落后潮头1.8千米共需多长时间？（潮水加速阶段速度
，
是加速前的速度）．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
