
【题目】如图1,平面内,![]() ,
,![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)当![]() 时,取
时,取![]() 的中点分别为
的中点分别为![]() ,连接
,连接![]() ,如图2,判断
,如图2,判断![]() 的形状,并加以证明.
的形状,并加以证明.
【答案】(1)证明见解析;(2)△AMN为等腰直角三角形,证明见解析.
【解析】
(1)由![]() 可得
可得![]() ,根据
,根据![]() ,
,![]() ,
,![]() ,利用SAS即可判定△ACD≌△ABE即可解决问题;
,利用SAS即可判定△ACD≌△ABE即可解决问题;
(2)先根据SAS判定△ABM≌△ACN,再根据全等三角形的性质,得出AM=AM,∠CAN=∠BAM,最后根据∠BAC=90°即可得到∠MAN=90°,进而得到△AMN为等腰直角三角形.
(1)如图1,∵![]() ,
,
∴![]() ,
,
在△DAC和△BAE中,
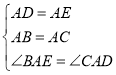 ,
,
∴△DAC≌△BAE(SAS),
∴![]() ;
;
(2)△AMN为等腰直角三角形.
证明:由(1)可得,BE=CD,
∵CD,BE的中点分别为点N、M,
∴BM=CN,
∵△DAC≌△BAE,
∴∠ABM=∠ACN,
在△ABM和△ACN中,
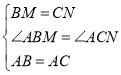 ,
,
∴△ABM≌△ACN(SAS),
∴AM=AN,且∠BAM=∠CAN,
又∵∠CAN+∠NAB=90°,
∴∠MAB+∠BAN=90°,
∴∠MAN=90°,
∴△AMN为等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】如图①,M是铁丝AD的中点,将该铁丝首尾相接折成△ABC(如图②),且∠B=30°,∠C=100°,则下列说法正确的是( )
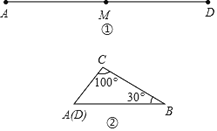
A. 点M在AB上B. 点M在BC上,且距点B较近,距点C较远
C. 点M在BC的中点处D. 点M在BC上,且距点C较近,距点B较远
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格中,小格的顶点叫做格点。小华按下列要求作图:①在正方形网格的三条不同的实线上各取一个格点,使其中任意两点不在同一条实线上;②连结三个格点,使之构成直角三角形。小华在左边的正方形网格中作出了Rt⊿ABC。请你按照同样的要求,在右边的两个正方形网格中各画出一个直角三角形,并使三个网格中的直角三角形互不全等。

查看答案和解析>>
科目:初中数学 来源: 题型:
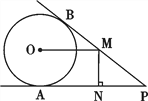
【题目】如图,PA,PB分别与⊙O相切于点A,B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.
(1)求证:OM = AN;
(2)若⊙O的半径R = 3,PA = 9,求OM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价![]() 元。据此规律,请回答:
元。据此规律,请回答:
(1)商场日销售量增加_____件,每件商品盈利_____元(用含![]() 的代数式表示)。
的代数式表示)。
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O的直径AB=20,将半圆O绕点B顺针旋转45°得到半圆O′,与AB交于点P.
(1)求AP的长;
(2)求图中阴影部分的面积(结果保留π).


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状,并说明你的理由;
(2)线段BD、DE、EC三者有什么关系?写出你的判断过程.
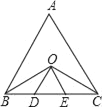
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)光伏发电惠民生,据衢州晚报载,某家庭投资4万元资金建造屋顶光伏发电站,遇到晴天平均每天可发电30度,其他天气平均每天可发电5度.已知某月(按30天计)共发电550度.
(1)求这个月晴天的天数;
(2)已知该家庭每月平均用电量为150度,若按每月发电550度计,至少需要几年才能收回成本.(不计其他费用,结果取整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,![]() ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)求∠BAC的度数;
(2)当点D在AB上方,且CD⊥BP时,求证:PC=AC;
(3)在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD,DE,直接写出△BDE的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com