
| A、18件 | B、19件 |
| C、20件 | D、21件 |
|
|
| 5 |
| 9 |
| 3 |
| 4 |


科目:初中数学 来源: 题型:
 窗台高1.2米,该地区冬天中午12时阳光从正南方照射时,光线与水平线的最小夹角为30°.
窗台高1.2米,该地区冬天中午12时阳光从正南方照射时,光线与水平线的最小夹角为30°.查看答案和解析>>
科目:初中数学 来源: 题型:
 你喜欢运动吗?请看以下两道根据体育运动编写的题目.
你喜欢运动吗?请看以下两道根据体育运动编写的题目.
|

查看答案和解析>>
科目:初中数学 来源: 题型:
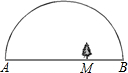 方案设计:儿童公园有一块半圆形空地,如图11所示,根据需要欲在此半圆内划出一个三角形区域作为健身场地,其中内接于此三角形的矩形区域为儿童游乐场,已知半圆的直径AB=100米,若使三角形的顶点C在半圆上,且AC=80米.
方案设计:儿童公园有一块半圆形空地,如图11所示,根据需要欲在此半圆内划出一个三角形区域作为健身场地,其中内接于此三角形的矩形区域为儿童游乐场,已知半圆的直径AB=100米,若使三角形的顶点C在半圆上,且AC=80米.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com