Question

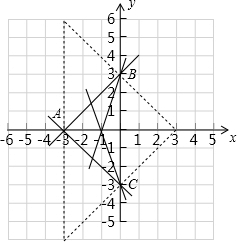
一次函数y=x+3与y=-x+q的图象都过点A（m，0），且与y轴分别交于点B、C．
（1）试求△ABC的面积；
（2）点D是平面直角坐标系内的一点，且以点A、C、B、D为顶点的四边形是平行四边形，请直接写出点D的坐标；
（3）过△ABC的顶点能否画一条直线，使它能平分△ABC的面积？若能，求出直线的函数关系式，若不能，说明理由．

Answer 1

分析：（1）将点A（m，0）代入y=x+3中求m的值，再将A点坐标代入y=-x+q中求q，从而可求两函数图象与y轴交点B、C的坐标，再计算△ABC的面积；
（2）AB、BC、CA都有可能作为平行四边形的对角线，故满足条件的D点坐标有三个；
（3）用△ABC的中线所在的直线将△ABC的面积平分．

解答：解：（1）将点A（m，0）代入y=x+3中，得
m+3=0，解得m=-3，即点A（-3，0），
将点A（-3，0）代入y=-x+q中，得q=-3，
∴点B（0，3）、C（0，-3），
故S=

1

2

×BC×AO=9；

（2）满足条件的D点坐标为D（-3，6）、D（-3，-6）、D（3，0）；

（3）若过点A，则得直线l：y=0；
若过点C，则得直线l：y=-3x-3；
若过点B，则得直线l：y=3x+3．

点评：本题考查了待定系数法求直线的解析式，根据平行四边形的性质确定点的方法及中线的性质．