
分析 在平面直角坐标系中,在y轴上取点P(0,1),过P作直线l∥x轴,作CM⊥OA于M,作CN⊥l于N,构造Rt△BCN≌Rt△ACM,得出CN=CM,若连接CP,则点C在∠BPO的平分线上,进而得出动点C在直线CP上运动;再分两种情况讨论C的路径端点坐标:①当m=-5时,②当m=5时,分别求得C(-1,0)和C1(4,5),而C的运动路径长就是CC1的长,最后由勾股定理可得CC1的长度.
解答 解:如图1所示,在y轴上取点P(0,1),过P作直线l∥x轴,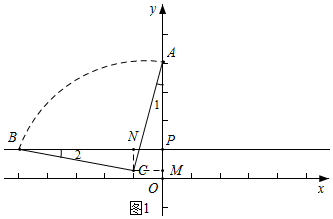
∵B(m,1),
∴B在直线l上,
∵C为旋转中心,旋转角为90°,
∴BC=AC,∠ACB=90°,
∵∠APB=90°,
∴∠1=∠2,
作CM⊥OA于M,作CN⊥l于N,则Rt△BCN≌Rt△ACM,
∴CN=CM,
若连接CP,则点C在∠BPO的平分线上,
∴动点C在直线CP上运动;
如图2所示,∵B(m,1)且-5≤m≤5,
∴分两种情况讨论C的路径端点坐标,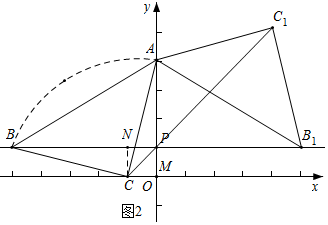
①当m=-5时,B(-5,1),PB=5,
作CM⊥y轴于M,作CN⊥l于N,
同理可得△BCN≌△ACM,
∴CM=CN,BN=AM,
可设PN=PM=CN=CM=a,
∵P(0,1),A(0,4),
∴AP=3,AM=BN=3+a,
∴PB=a+3+a=5,
∴a=1,
∴C(-1,0);
②当m=5时,B(5,1),如图2中的B1,此时的动点C是图2中的C1,
同理可得C1(4,5),
∴C的运动路径长就是CC1的长,
由勾股定理可得,CC1=$\sqrt{[4-(-1)]^{2}+{5}^{2}}$=$\sqrt{50}$=5$\sqrt{2}$.
点评 本题主要考查了旋转图形的坐标、全等三角形的判定与性质以及轨迹的运用,解题时注意:图形或点旋转之后要结合旋转的角度和图形的特殊性质,求出旋转后的点的坐标.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 李老师用直尺和圆规作已知角的平分线.
李老师用直尺和圆规作已知角的平分线.| A. | SSS | B. | SAS | C. | ASA | D. | AAS |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 数量x(千克) | 售价c(元) |
| 1 | 14+1.2 |
| 2 | 28+2.4 |
| 5 | 70+6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com