
如图,点P是正方形ABCD内的一点,若PA=a,PB=2a,PC=3a(a>0).求:
(1)∠APB的度数;
(2)正方形的边长.

|
解:(1)将△APB绕点B顺时针旋转 △CQB≌△APB. ∵∠PBQ=∠PBC+∠CBQ=∠PBC+∠PBA= PB=QB=2a, ∴∠PQB=∠BPQ= 在△PQC中, PC=3a,QC=PA=a,PQ=2 ∴PC2=CQ2+PQ2. ∴∠PQC= ∴∠APB=∠CQB=∠PQB+∠PQC= (2)由(1)得 ∠APB+∠BPQ= ∴A、P、Q三点共线. ∴AQ=AP+PQ=a+2 在Rt△AQC中, AC= = =a· ∴正方形ABCD的边长为 AB= |
|
点悟:题目中已知长度的三条线段位于三个不同的三角中,为使其集中起来,可考虑采用旋转的方式. 点拨:一般地,在问题中若含有相等的线段和角,或含有一些特殊角(如等边三角形、正方形等)时,常利用旋转变换,将已知的条件集中到一起,实现相对集中的原则. |


科目:初中数学 来源: 题型:
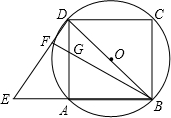 如图,点E是正方形ABCD边BA延长线上一点(AE<AD),连接DE.与正方形ABCD的外接圆相交于点F,BF与AD相交于点G.
如图,点E是正方形ABCD边BA延长线上一点(AE<AD),连接DE.与正方形ABCD的外接圆相交于点F,BF与AD相交于点G.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•包头)如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C=
(2013•包头)如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C=查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点E是正方形ABCD边BC的中点,H是BC延长线上的一点,EG⊥AE于点E,交边CD于G,
如图,点E是正方形ABCD边BC的中点,H是BC延长线上的一点,EG⊥AE于点E,交边CD于G,查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点M是正方形ABCD的边CD的中点,正方形ABCD的边长为4cm,点P按A-B-C-M-D的顺序在正方形的边上以每秒1cm的速度作匀速运动,设点P的运动时间为x(秒),△APM的面积为y(cm2)
如图,点M是正方形ABCD的边CD的中点,正方形ABCD的边长为4cm,点P按A-B-C-M-D的顺序在正方形的边上以每秒1cm的速度作匀速运动,设点P的运动时间为x(秒),△APM的面积为y(cm2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com