
分析 (1)利用配方法或公式法解方程即可;
(2)利用因式分解法和直接开平方解方程即可;
(3)利用因式分解法或公式法解方程即可.
解答 解:(1)解一:∵x2-6x+9+1=9;
∴(x-3)2=8,
∴x-3=±2$\sqrt{2}$,
∴x1=3+2$\sqrt{2}$,x2=3-2$\sqrt{2}$;
解二:∵a=1,b=-6,c=1,
∴b2-4ac=32>0,
∴x=$\frac{6±\sqrt{32}}{2}$,
∴x=3±2$\sqrt{2}$,
∴x1=3+2$\sqrt{2}$,x2=3-2$\sqrt{2}$;
(2)解一:∵( x+1)2-4x2=0,
∴(x+1+2x) (x+1-2x)=0,
∴(3x+1)(1-x)=0,
∴3x+1=0或1-x=0,
∴x1=-$\frac{1}{3}$,x2=1.
解二:∵(x+1)2=4x2,
∴x+1=±2x,
∴3x+1=0或-x+1=0,
∴x1=-$\frac{1}{3}$,x2=1.
(3)解一:∵3x(2x+1)=2(2x+1),
∴3x(2x+1)-2(2x+1)=0
∴(2x+1)(3x-2)=0,
∴x1=-$\frac{1}{2}$,x2=$\frac{2}{3}$.
解二:∵3x(2x+1)=2(2x+1),
∴6x2-x-2=0,
∴x=$\frac{1±\sqrt{25}}{2×6}$,
∴x1=-$\frac{1}{2}$,x2=$\frac{2}{3}$.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
| ①始发站 | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩终点站 | |
| 上客人数 | 9 | 8 | 10 | 12 | 14 | 13 | 11 | 6 | 7 | 0 |
| 下客人数 | 0 | -3 | -5 | -7 | -4 | -8 | -6 | -9 | x | -28 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,∠ABC=45°,高AD、BE相交于点F,CD=4,则线段DF的长为( )
如图,△ABC中,∠ABC=45°,高AD、BE相交于点F,CD=4,则线段DF的长为( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 3$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
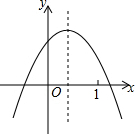 已知二次函数y=ax2+bx+c的图象如图所示,则下列选项中不正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列选项中不正确的是( )| A. | a<0 | B. | c>0 | C. | 0<-$\frac{b}{2a}$<1 | D. | a+b+c<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com