
【题目】设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+3上的三点,则y1 , y2 , y3的大小关系为( )
A.y1>y2>y3
B.y1>y3>y2
C.y3>y2>y1
D.y3>y1>y2
科目:初中数学 来源: 题型:
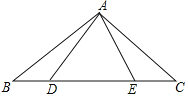
【题目】如图,点D,E在△ABC的边BC上,连接AD,AE.有下面三个等式:①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,相构成三个命题.解答下列问题
(1)写出这三个命题,并直接判断其是否是真命题;
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE
(1)判断OF与OD的位置关系,并进行证明.
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(3,1),B(8,5),若用(3,1)→(3,3)→(5,3)→(5,4)→(8,4)→(8,5)表示由A到B的一种走法,并规定从A到B只能向上或向右走,请用上述表示法写出另两种走法,并判断这几种走法的路程是否相等。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下面的程序计算:当输入x=100 时,输出结果是299;当输入x=50时,输出结果是446;如果输入 x 的值是正整数,输出结果是257,那么满足条件的x的值最多有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC内部一个动点,∠APB=120°,⊙O是△APB的外接圆.AP,BP的延长线分别交BC,AC于D,E. 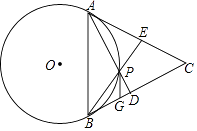
(1)求证:CA,CB是⊙O的切线;
(2)已知AB=6,G在BC上,BG=2,当PG取得最小值时,求PG的长及∠BGP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一块瓷砖的图案,用这种瓷砖来铺设地面,如果铺成一个2×2的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个3×3的正方形图案(如图③),其中完整的圆共有13个,如果铺成一个4×4的正方形图案(如图④),其中完整的圆共有25个,若这样铺成一个10×10的正方形图案,则其中完整的圆共有( )个.
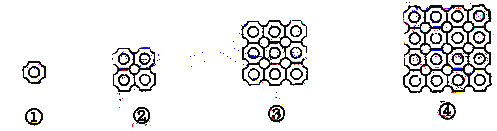
A.145 B.146 C.180 D.181
查看答案和解析>>
科目:初中数学 来源: 题型:
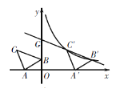
【题目】如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0),B(0,1),C(d,2).
(1)求d的值;
(2)将△ABC沿x轴的正方向平移,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图象上. 请求出这个反比例函数和此时的直线B′C′的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,火车站、码头分别位于A,B两点,直线a和b分别表示铁路与河流.

(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com