
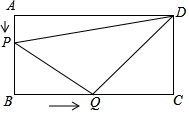
 如图所示,在长方形ABCD中,AB=6厘米,BC=12厘米,点P沿AB边从点A开始向点B以1厘米/秒的速度移动,点Q沿BC从点B开始向点C以2厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).
如图所示,在长方形ABCD中,AB=6厘米,BC=12厘米,点P沿AB边从点A开始向点B以1厘米/秒的速度移动,点Q沿BC从点B开始向点C以2厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).分析 (1)由AB、PB的长可求得AP的长,则可求得t的值;
(2)根据等腰直角三角形的性质可求得PB=BQ,则可得到关于t的方程,可求得t的值;
(3)可用t分别表示出S△APD、S△QCD,再利用面积的和差可求得四边形PBQD的面积,则可求得结论.
解答 解:
(1)∵PB=2cm,AB=6cm,
∴AP=AB-PB=6-2=4(秒),
即点P移动4秒;
(2)∵△PBQ为等腰直角三角形,
∴PB=BQ,即6-t=2t,解得t=2
∴当t的值为2秒时,△PBQ为等腰直角三角形;
(3)由题意可知AP=t,AB=6,BQ=2t,BC=12,
∴PB=6-t,QC=12-2t,CD=6,AD=12,
∴S△APD=$\frac{1}{2}$AP•AD=$\frac{1}{2}$t×12=6t,S△QCD=$\frac{1}{2}$QC•CD=$\frac{1}{2}$(12-2t)6=36-6t,
∴S四边形PBQD=S矩形ABCD-S△APD-S△QCD=72-6t-(36-6t)=36,
结论:不论P、Q怎样运动总有四边形PBQD的面积等于长方形ABCD面积的一半.
点评 本题为四边形的综合应用,涉及等腰三角形的性质、三角形的面积、方程思想及转化思想.用t表示出相应线段的长度,化动为静是解决这类运动型问题的一般思想.本题考查知识点不是太多,难度不大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 没有加减运算的代数式是单项式 | B. | 单项式$\frac{3{x}^{2}y}{4}$的系数是3,次数是2 | ||
| C. | 单项式x既没有系数,也没有次数 | D. | 单项式-a2bc的系数是-1,次数是4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
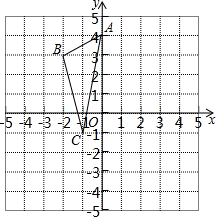 如图,网格中每个小正方形的边长均为1,已知三角形ABC及三角形外一点D,平移三角形ABC使点A(0,4)移动到点D(3,2),得到三角形DEF,B(-2,3)的对应点为E,C(-1,-1)对应点F.
如图,网格中每个小正方形的边长均为1,已知三角形ABC及三角形外一点D,平移三角形ABC使点A(0,4)移动到点D(3,2),得到三角形DEF,B(-2,3)的对应点为E,C(-1,-1)对应点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,若∠DAE=∠E,∠B=∠D,那么AB∥DC吗?请在下面的解答过程中填空或在括号内填写理由.
如图,若∠DAE=∠E,∠B=∠D,那么AB∥DC吗?请在下面的解答过程中填空或在括号内填写理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com