
��ͼ��ij���۹��������ص�EΪ�ļ���Ŀ�������㣬��֪��E������������AB�ľ���OEΪ10�ף�����ABΪ123��(AB��ֱ����BC)���ڵ���C����õ�E�����Ǧ���45�㣬�ӵ�C��CB����ǰ��40����D�㣬��D���������A�����Ǧ£�60�㣬���E�����ĸ߶�EF.(�����ȷ��1�ף��ο����� ��1.4��
��1.4�� 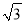 ��1.7)
��1.7)

 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���㶫ʡ��ݸ�к���ѧУ2017-2018ѧ����꼶���ϣ�������ѧ�Ծ���word�溬�𰸽����� ���ͣ������
��֪��2xm��2y2��3x4y2m+n��ͬ�����m��3n��ƽ������_____��
��6 �����������������ͬ������ָ������ĸ��ͬ������ͬ��ĸ��ָ��Ҳ��ͬ����������ʽ�����ݶ����֪�� ����ã� ����m-3n=6+30=36����m-3n��ƽ����Ϊ�� ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ���ݵ���2017-2018ѧ��Ⱦ��꼶��һѧ����ĩ�����ѧ�Ծ� ���ͣ���ѡ��
��ͼ���� �������������У�ÿ��С�����εı߳�Ϊ1������
�������������У�ÿ��С�����εı߳�Ϊ1������ �Ƶ�O˳ʱ����ת90��õ�
�Ƶ�O˳ʱ����ת90��õ� ����
���� �ij��� ��
�ij��� ��

A.  B. 6
B. 6 C. 3
C. 3 D. 1.5
D. 1.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ����ʮ���´����� ���ͣ���ѡ��
��ͼ��ֱ��y=kx+b��x�ᡢy��ֱ��ཻ�ڵ�A����3��0����B��0��2������ʽkx+b��0�Ľ⼯�ǣ� ��

A. x����3 B. x����3 C. x��2 D. x��2
A ���������ȸ��ݺ���y=kx+b��x��Ľ��㣨-3��0������֪kx+b��0�Ľ⼯Ϊx��-3. ��ѡ��A.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ����ʮ���´����� ���ͣ���ѡ��
һ�κ���y����3x��2��ͼ������ ��
A. ��һ���� B. �ڶ����� C. �������� D. ��������
A ���������������������һ�κ��������ʣ���k��0ʱ��ͼ����һ��������� ��k=2��0�� �ຯ��������һ�������ޣ� ��b=��3��0���ຯ����y�Ḻ�����ཻ�� ��ͼ�����ڶ����ޣ� ��ѡ��B�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ���ڶ�ʮ���� ������ ���ͣ������
���㣺��1��2sin 30�㣫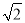 cos 45�㣭
cos 45�㣭 tan 60�㣻��2��tan230�㣫cos230�㣭sin245��tan 45��.
tan 60�㣻��2��tan230�㣫cos230�㣭sin245��tan 45��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ���ڶ�ʮ���� ������ ���ͣ���ѡ��
��ͼ����ABC�ǵȱ������Σ���D��BC��������һ�㣬DE��AB�ڵ�E��DF��AC�ڵ�F.��BC��2����DE��DF��(����)

A. 1 B. 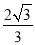 C.
C. 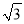 D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�ܿ���������2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
�۲����и�ʽ�Ĺ��ɣ�

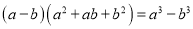

����
�ɵõ� _______��
_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
����������12�֣���ͼ��Rt�� �У�
��  ��
��  ����
���� Ϊб��
Ϊб�� ���е㣬��
���е㣬�� Ϊ��
Ϊ�� �ϵ�һ�����㣮����
�ϵ�һ�����㣮���� ������
������ ��
�� �Ĵ������
�Ĵ������ ���ڵ�
���ڵ� ����
���� Ϊ�ڱ�������
Ϊ�ڱ������� ��
��

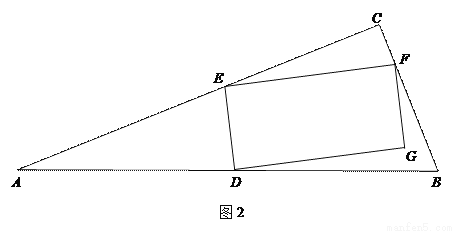
��1����ͼ1���� ����
���� �ڱ�
�ڱ�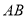 ��ʱ����DE��EF�ij���
��ʱ����DE��EF�ij���
��2����ͼ2����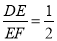 ����
���� ������
������ �����Ϊ
�����Ϊ ����y����
����y���� �ĺ�������ʽ��
�ĺ�������ʽ��
��3���� ���ҵ�
���ҵ� ǡ������Rt��
ǡ������Rt�� �ı��ϣ���
�ı��ϣ��� �ij���
�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com