
【题目】如图,AB是⊙O的直径,AC为弦,∠BAC的平分线交⊙O于点D,过点D的切线交AC的延长线于点G.
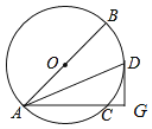
求证:(1)DG⊥AG;
(2)AG+CG=AB.
【答案】见解析
【解析】
(1)连接OD,根据等腰三角形的性质结合角平分线的性质可得出∠CAD=∠ODA,利用“内错角相等,两直线平行”可得出AE∥OD,结合切线的性质即可证出DG⊥AG;
(2)过点D作DM⊥AB于点M,连接CD、DB,根据角平分线的性质可得出DG=DM,
结合AD=AD、∠AGD=∠AMD=90°即可证出△DAG≌△DAM(SAS),根据全等三角形的性质可得出AG=AM,由∠GAD=∠MAD可得出![]() =
= ![]() ,进而可得出CD=BD,结合DG=DM可证出Rt△DGC≌Rt△DMB(HL),根据全等三角形的性质可得出CG=BM,结合AB=AM+BM即可证出AG+CG=AB.
,进而可得出CD=BD,结合DG=DM可证出Rt△DGC≌Rt△DMB(HL),根据全等三角形的性质可得出CG=BM,结合AB=AM+BM即可证出AG+CG=AB.
(1)连接OD,
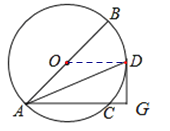
OA=OD,
∠OAD=∠ODA,
DA平分∠BAC,
则∠OAD=∠CAD,
![]() ∠CAD=∠ODA,
∠CAD=∠ODA,
![]() AE∥OD,
AE∥OD,
DG是⊙O的切线,则![]()
![]() DG⊥AG;
DG⊥AG;
(2)过点D作DM⊥AB于点M,连接CD、DB,
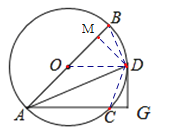
DA平分∠BAC,
DG=DM,
结合AD=AD、∠AGD=∠AMD=90°,
△DAG≌△DAM(SAS),
AE=AM,
由∠GAD=∠MAD,
![]() =
= ![]() ,
,
![]() CD=BD,结合DG=DM可证出Rt△DGC≌Rt△DMB(HL),
CD=BD,结合DG=DM可证出Rt△DGC≌Rt△DMB(HL),
CG=BM,
![]() AB=AM+BM,
AB=AM+BM,
![]() AG+CG=AB.
AG+CG=AB.


科目:初中数学 来源: 题型:
【题目】注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路,填写表格,并完成本题解答的全过程.如果你选用其他的解题方案,此时,不必填写表格, 只需按照解答题的一般要求,进行解答即可.
某校八年级学生由距博物馆 10km 的学校出发前往参观,一部分同学骑自行车先走,过了20min 后,其余同学乘汽车出发,结果他们同时到达.已知汽车的速度是骑车同学速度 的 2 倍,求骑车同学的速度.
设骑车同学的速度为 xkm / h
(Ⅰ)根据题意,利用速度、时间、路程之间的关系,用含有 x 的式子填写下表:
速度(千米 / 时) | 所用时间(时 ) | 所走的路程(千米) | |
骑自行车 | x | 10 | |
乘汽车 | 10 |
(Ⅱ)列出方程,并求出问题的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(1)求反比例函数的解析式及B点的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射击队为了解运动员的年龄情况,作了一次年龄调查,根据射击运动员的年龄(单位:岁),绘制出如图的统计图.
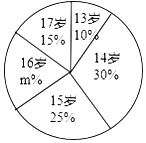
(1)求m的值;
(2)该射击队运动员年龄是众数是 .
(3)求该射击队运动员的平均年龄;
(4)若该射击队有13岁运动员2人,则该射击队中14岁运动员有几人?
查看答案和解析>>
科目:初中数学 来源: 题型:
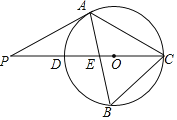
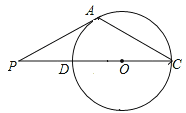
【题目】如图,△ABC内接于⊙O,CD是⊙O的直径,AB与CD交于点E,点P是CD延长线上的一点,AP=AC,且∠B=2∠P.
(1)求证:∠B=2∠PCA.
(2)求证:PA是⊙O的切线;
(3)若点B位于直径CD的下方,且CD平分∠ACB,试判断此时AE与BE的大小关系,并说明由.
查看答案和解析>>
科目:初中数学 来源: 题型:
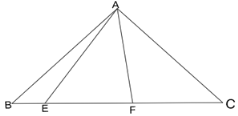
【题目】已知:如图,等腰直角三角形ABC中,∠BAC=90°,BA=AC,点E、F是线段BC上两动点且∠EAF=45°,请写出BE、EF、FC之间的等量关系并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com