设y＝y1＋y2，在下列各题中，求y关于x的函数解析式：
(1)y1、y2都与x成正比例，且x＝2时，y＝－1；
(2)y1、y2都与x成反比例，且x＝
时，y＝1；
(3)y1与x成正比例，y2与x成反比例，且x＝1时，y＝2；x＝2时，y＝－
．
阅读快车系列答案科目：初中数学 来源： 题型：阅读理解
请同学们认真阅读下面材料，然后解答问题。（6分）
解方程（x2－1）2－5（x－1）＋4＝0
解：设y＝x2－1
则原方程化为：y2－5y＋4＝0 ① ∴y1＝1 y2＝4
当y＝1时，有x2－1＝1，即x2＝2 ∴x＝±
当y＝4时，有x2－1＝4，即x2＝5 ∴x＝±
∴原方程的解为：x1＝－ x2＝
x3＝－
x4＝
解答问题：
⑴填空：在由原方程得到①的过程中，利用________________法达到了降次的目的，体现了________________的数学思想。
⑵解方程－3（
－3）＝0
查看答案和解析>>
科目：初中数学 来源：2012-2013学年江苏泰兴实验初级中学八年级上期末考试数学试卷（带解析） 题型：解答题
在一条笔直的河道上依次有A、B、C三个港口，甲、乙两船同时分别从A、B 港口出发，沿直线匀速驶向C港，最终到达C港．设甲、乙两船行驶x(h)后，与B港的距离分别为y1、y2(km)，y1、y2与x的函数关系如图所示(点P、Q为图象的交点)．
（1）填空：A、C两港口间的距离为 km，a＝ ；
（2）求y1与x的函数关系式，并写出自变量x的取值范围；
（3）求图中点P的坐标，并解释该点坐标所表示的实际意义。
查看答案和解析>>
科目：初中数学 来源：2012-2013学年浙江省桐乡市九年级文理联赛模拟卷数学试卷（解析版） 题型：解答题
如图1，在Rt△ABC中，∠C＝90°，BC＝8厘米，点D在AC上，CD＝3厘米．点P、Q分别由A、C两点同时出发，点P沿AC方向向点C匀速移动，速度为每秒k厘米，行完AC全程用时8秒；点Q沿CB方向向点B匀速移动，速度为每秒1厘米．设运动的时间为x秒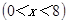
，△DCQ的面积为y1平方厘米，△PCQ的面积为y2平方厘米．
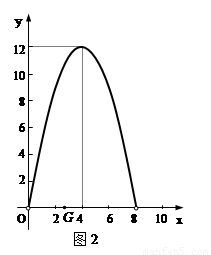
（1）求y1与x的函数关系，并在图2中画出y1的图象；
（2）如图2，y2的图象是抛物线的一部分，其顶点坐标是（4，12），求点P的速度及AC的长；
（3）在图2中，点G是x轴正半轴上一点（0＜OG＜6），过G作EF垂直于x轴，分别交y1、y2于点E、F．
①说出线段EF的长在图1中所表示的实际意义；
②当0＜x＜６时，求线段EF长的最大值．
查看答案和解析>>
科目：初中数学 来源：2010-2011学年江苏省兴化市初三第一学期12月月考数学卷 题型：解答题
请同学们认真阅读下面材料，然后解答问题。（6分）
解方程（x2－1）2－5（x－1）＋4＝0
解：设y＝x2－1
则原方程化为：y2－5y＋4＝0 ① ∴y1＝1 y2＝4
当y＝1时，有x2－1＝1，即x2＝2 ∴x＝±
当y＝4时，有x2－1＝4，即x2＝5
∴x＝±
∴原方程的解为：x1＝－ x2＝ x3＝－ x4＝
解答问题：
⑴填空：在由原方程得到①的过程中，利用________________法达到了降次的目的，体现了________________的数学思想。
⑵解方程
－3（
－3）＝0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
x．(先需分别求出k1和k2)
(k1≠0)，y2＝
(k2≠0)∴y＝y1＋y2＝
＋
＝
，
时，y＝1，∴k1＋k2＝xy＝
×1＝
，∴y＝
．
(k2≠0)，∴y＝k1x＋
，
∴
x＋
．
