
”¾ĢāÄæ”æ“ÓČż½ĒŠĪŅ»øö¶„µćŅż³öŅ»ĢõÉäĻßÓė¶Ō±ßĻą½»£¬¶„µćÓė½»µćÖ®¼äµÄĻ߶Ī°ŃÕāøöČż½ĒŠĪ·Öøī³ÉĮ½øöŠ”Čż½ĒŠĪ£¬Čē¹ū·ÖµĆµÄĮ½øöŠ”Čż½ĒŠĪÖŠŅ»øöĪŖµČŃüČż½ĒŠĪ£¬ĮķŅ»øöÓėŌČż½ĒŠĪĻąĖĘ£¬ĪŅĆĒ°ŃÕāĢõĻ߶Ī½Š×öÕāøöČż½ĒŠĪµÄÓÅĆĄĻߣ®
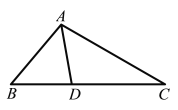
£Ø1£©ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬ADĪŖ½ĒĘ½·ÖĻߣ¬”ĻB=50”ć£¬”ĻC=30”ć£¬ĒóÖ¤£ŗADĪŖ”÷ABCµÄÓÅĆĄĻߣ»
£Ø2£©ŌŚ”÷ABCÖŠ£¬”ĻB=46”ć£¬ADŹĒ”÷ABCµÄÓÅĆĄĻߣ¬ĒŅ”÷ABDŹĒŅŌABĪŖŃüµÄµČŃüČż½ĒŠĪ£¬Ēó”ĻBACµÄ¶ČŹż£®
”¾“š°ø”æ£Ø1£©¼ū½āĪö£»£Ø2£©”ĻBACµÄ¶ČŹżĪŖ113”ć£®
”¾½āĪö”æ
±¾ĢāŹĒŅ»µĄŠĀ¶ØŅåĶ¼ŠĪµÄĢā”£
£Ø1£©øł¾ŻČż½ĒŠĪµÄÓÅĆĄĻߵĶØŅ壬ֻŅŖÖ¤Ć÷”÷ABDŹĒµČŃüČż½ĒŠĪ£¬”÷CAD”×”÷CBA¼“æɽā¾öĪŹĢā£®
£Ø2£©ČēĶ¼2ÖŠ£¬·ÖĮ½ÖÖĒéŠĪĢÖĀŪĒó½ā¢ŁČōAB=AD£¬”÷CAD”×”÷CBA£¬Ōņ”ĻB=”ĻADB=”ĻCAD£¬ŌņAC”ĪBC£¬ÕāÓė”÷ABCÕāøöĢõ¼žĆ¬¶Ü£»¢ŚČōAB=BD£¬”÷CAD”×”÷CBA.
£Ø1£©Ö¤Ć÷£ŗ”ß![]() £¬
£¬![]() £¬
£¬
”ą![]() .
.
”ßADĪŖ½ĒĘ½·ÖĻߣ¬
”ą![]() .
.
”ą![]() .
.
”ą![]() .
.
”ą”÷ABDŹĒµČŃüČż½ĒŠĪ.
”ß![]() £¬
£¬![]() £¬
£¬
”ą”÷CAD”×”÷CBA.
”ąADĪŖ”÷ABCµÄÓÅĆĄĻߣ®
£Ø2£©”ßADŹĒ”÷ABCµÄÓÅĆĄĻߣ¬ĒŅ”÷ABDŹĒŅŌABĪŖŃüµÄµČŃüČż½ĒŠĪ£¬
”ą”÷CAD”×”÷CBA.
”ą![]() .
.
”ß”÷ABDŹĒŅŌABĪŖŃüµÄµČŃüČż½ĒŠĪ£¬
·ÖĮ½ÖÖĒéæö:
µ±AB=ADŹ±£¬
”ą![]() .
.
ÓÖ”ß![]() £¬
£¬
”ą![]() £¬²»·ūŗĻĢāŅā£¬ÕāÖÖĒéæö²»“ęŌŚ.
£¬²»·ūŗĻĢāŅā£¬ÕāÖÖĒéæö²»“ęŌŚ.
µ±AB=BDŹ±£¬
”ą![]() .
.
”ą![]() .
.
”ą”ĻBACµÄ¶ČŹżĪŖ![]() £®
£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµ![]() ÖŠ£¬¶ž“ĪŗÆŹż
ÖŠ£¬¶ž“ĪŗÆŹż![]() µÄ¶Ō³ĘÖįĪŖ
µÄ¶Ō³ĘÖįĪŖ![]() £®µć
£®µć![]() ŌŚÖ±Ļß
ŌŚÖ±Ļß![]() ÉĻ.
ÉĻ.
£Ø1£©Ēó![]() £¬
£¬ ![]() µÄÖµ£»
掙术
£Ø2£©Čōµć![]() ŌŚ¶ž“ĪŗÆŹż
ŌŚ¶ž“ĪŗÆŹż![]() ÉĻ£¬Ēó
ÉĻ£¬Ēó![]() µÄÖµ£»
掙术
£Ø3£©µ±¶ž“ĪŗÆŹż![]() ÓėÖ±Ļß
ÓėÖ±Ļß![]() Ļą½»ÓŚĮ½µćŹ±£¬Éč×ó²ąµÄ½»µćĪŖ
Ļą½»ÓŚĮ½µćŹ±£¬Éč×ó²ąµÄ½»µćĪŖ![]() £¬Čō
£¬Čō![]() £¬Ēó
£¬Ēó![]() µÄȔֵ·¶Ī§£®
µÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
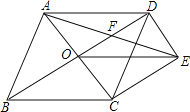
”¾ĢāÄæ”æČēĶ¼£¬ĮāŠĪABCDµÄ¶Ō½ĒĻßAC”¢BDĻą½»ÓŚµćO£¬¹żµćD×÷DE”ĪAC£¬ĒŅDE£½![]() AC£¬Į¬½ÓCE”¢OE£¬Į¬½ÓAE½»ODÓŚµćF£®
AC£¬Į¬½ÓCE”¢OE£¬Į¬½ÓAE½»ODÓŚµćF£®
£Ø1£©ĒóÖ¤£ŗOE£½CD£»
£Ø2£©ČōĮāŠĪABCDµÄ±ß³¤ĪŖ8£¬”ĻABC£½60”ć£¬ĒóAEµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ·“±ČĄżŗÆŹży£½©![]() £¬ĻĀĮŠ½įĀŪ£ŗ¢ŁĶ¼Ļó±Ų¾¹żµć£Ø©3£¬1£©£»¢ŚĶ¼ĻóŌŚµŚ¶ž£¬ĖÄĻóĻŽÄŚ£»¢ŪyĖęxµÄŌö“ó¶ųŌö“󣻢ܵ±x£¾©1Ź±£¬y£¾3£®ĘäÖŠ“ķĪóµÄ½įĀŪÓŠ£Ø””””£©
£¬ĻĀĮŠ½įĀŪ£ŗ¢ŁĶ¼Ļó±Ų¾¹żµć£Ø©3£¬1£©£»¢ŚĶ¼ĻóŌŚµŚ¶ž£¬ĖÄĻóĻŽÄŚ£»¢ŪyĖęxµÄŌö“ó¶ųŌö“󣻢ܵ±x£¾©1Ź±£¬y£¾3£®ĘäÖŠ“ķĪóµÄ½įĀŪÓŠ£Ø””””£©
A. ¢Ł¢Ü B. ¢Ś¢Ū C. ¢Ś¢Ü D. ¢Ū¢Ü
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶ŌÓŚ×Ō±äĮæxµÄ²»Ķ¬µÄȔֵ·¶Ī§£¬ÓŠ×Ų»Ķ¬µÄ¶ŌÓ¦¹ŲĻµ£¬ÕāŃłµÄŗÆŹżĶس£½Š×ö·Ö¶ĪŗÆŹż£®ĖüŹĒŅ»øöŗÆŹż£¬¶ų²»ŹĒ¼øøöŗÆŹż. ·Ö¶ĪŗÆŹżŌŚ×Ō±äĮæxµÄ²»Ķ¬µÄȔֵ·¶Ī§ÄŚ£¬ŗÆŹżµÄ±ķ“ļŹ½Ņ²²»Ķ¬£®ĄżČē£ŗ![]() ŹĒ·Ö¶ĪŗÆŹż£®
ŹĒ·Ö¶ĪŗÆŹż£®
µ±![]() Ź±£¬ĖüŹĒ¶ž“ĪŗÆŹż
Ź±£¬ĖüŹĒ¶ž“ĪŗÆŹż![]() £»µ±
£»µ±![]() Ź±£¬ĖüŹĒÕż±ČĄżŗÆŹż
Ź±£¬ĖüŹĒÕż±ČĄżŗÆŹż![]() £®
£®
£Ø1£©ĒėŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ»³öŗÆŹż![]() µÄĶ¼Ļó£»
µÄĶ¼Ļó£»
£Ø2£©Ēó³öyÖį×ó²ąĶ¼ĻóµÄ×īµĶµćµÄ×ų±ź£»
£Ø3£©µ±![]() Ź±£¬Ēó×Ō±äĮæxµÄÖµ£®
Ź±£¬Ēó×Ō±äĮæxµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=3£¬AC=4£¬BC=5£¬PĪŖ±ßBCÉĻŅ»¶Æµć£¬PE”ĶABÓŚE£¬PF”ĶACÓŚF£¬MĪŖEFÖŠµć£¬ŌņAMµÄ×īŠ”ÖµĪŖ_____£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£°ĖÄź¼¶Į½øö°ą£¬ø÷Ń”ÅÉ10Ćūѧɜ²Ī¼ÓѧŠ£¾ŁŠŠµÄ”°ŗŗ×ÖĢżŠ“”±“óČü£®ø÷²ĪČüŃ”ŹÖ³É¼ØµÄŹż¾Ż·ÖĪöČēĻĀ±ķĖłŹ¾£¬ŌņŅŌĻĀÅŠ¶Ļ“ķĪóµÄŹĒ£Ø””””£©
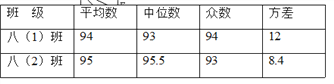
A. °Ė£Ø2£©°ąµÄ×Ü·ÖøßÓŚ°Ė£Ø1£©°ą B. °Ė£Ø2£©°ąµÄ³É¼Ø±Č°Ė£Ø1£©°ąĪȶØ
C. °Ė£Ø2£©°ąµÄ³É¼Ø¼ÆÖŠŌŚÖŠÉĻÓĪ D. Į½øö°ąµÄ×īøß·ÖŌŚ°Ė£Ø2£©°ą
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖµć![]() £¬
£¬![]() £¬µćCŹĒÖ±ĻßABÉĻŅģÓŚµćBµÄČĪŅ»µć£¬ĻÖŅŌBCĪŖŅ»±ßŌŚABÓŅ²ą×÷Õż·½ŠĪBCDE£¬ÉäĻßOCÓėÖ±ĻßDE½»ÓŚµćP£¬ČōµćCµÄŗį×ų±źĪŖm£®
£¬µćCŹĒÖ±ĻßABÉĻŅģÓŚµćBµÄČĪŅ»µć£¬ĻÖŅŌBCĪŖŅ»±ßŌŚABÓŅ²ą×÷Õż·½ŠĪBCDE£¬ÉäĻßOCÓėÖ±ĻßDE½»ÓŚµćP£¬ČōµćCµÄŗį×ų±źĪŖm£®

![]() ĒóÖ±ĻßABµÄŗÆŹż±ķ“ļŹ½£®
ĒóÖ±ĻßABµÄŗÆŹż±ķ“ļŹ½£®
![]() ČōµćCŌŚµŚŅ»ĻóĻŽ£¬ĒŅµćCĪŖOPµÄÖŠµć£¬ĒómµÄÖµ£®
ČōµćCŌŚµŚŅ»ĻóĻŽ£¬ĒŅµćCĪŖOPµÄÖŠµć£¬ĒómµÄÖµ£®
![]() ČōµćCĪŖOPµÄČżµČ·Öµć
ČōµćCĪŖOPµÄČżµČ·Öµć![]() ¼“µćC·ÖOP³É1£ŗ2µÄĮ½ĢõĻ߶Ī
¼“µćC·ÖOP³É1£ŗ2µÄĮ½ĢõĻ߶Ī![]() £¬ĒėÖ±½ÓŠ“³öµćCµÄ×ų±ź£®
£¬ĒėÖ±½ÓŠ“³öµćCµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬ĪŅĆĒŅŃ¾Ń§¹ż£ŗµćC½«Ļ߶ĪAB·Ö³ÉĮ½²æ·Ö£¬Čē¹ū![]() £¬ÄĒĆ“³ĘµćCĪŖĻ߶ĪABµÄ»Ę½š·Öøīµć£®Ä³Š£µÄŹżŃ§ĶŲÕ¹ŠŌæĪ³Ģ°ą£¬ŌŚ½ųŠŠÖŖŹ¶ĶŲÕ¹Ź±£¬ÕÅĄĻŹ¦ÓÉ»Ę½š·ÖøīµćĶŲÕ¹µ½”°»Ę½š·ÖøīĻß”±£¬ĄąĖʵŲøų³ö”°»Ę½š·ÖøīĻß”±µÄ¶ØŅå£ŗÖ±Ļßl½«Ņ»øöĆ껿ĪŖSµÄĶ¼ŠĪ·Ö³ÉĮ½²æ·Ö£¬ÕāĮ½²æ·ÖµÄĆ껿·Ö±šĪŖS1£¬S2£¬Čē¹ū
£¬ÄĒĆ“³ĘµćCĪŖĻ߶ĪABµÄ»Ę½š·Öøīµć£®Ä³Š£µÄŹżŃ§ĶŲÕ¹ŠŌæĪ³Ģ°ą£¬ŌŚ½ųŠŠÖŖŹ¶ĶŲÕ¹Ź±£¬ÕÅĄĻŹ¦ÓÉ»Ę½š·ÖøīµćĶŲÕ¹µ½”°»Ę½š·ÖøīĻß”±£¬ĄąĖʵŲøų³ö”°»Ę½š·ÖøīĻß”±µÄ¶ØŅå£ŗÖ±Ļßl½«Ņ»øöĆ껿ĪŖSµÄĶ¼ŠĪ·Ö³ÉĮ½²æ·Ö£¬ÕāĮ½²æ·ÖµÄĆ껿·Ö±šĪŖS1£¬S2£¬Čē¹ū![]() £¬ÄĒĆ“³ĘÖ±ĻßlĪŖøĆĶ¼ŠĪµÄ»Ę½š·ÖøīĻߣ®
£¬ÄĒĆ“³ĘÖ±ĻßlĪŖøĆĶ¼ŠĪµÄ»Ę½š·ÖøīĻߣ®
ČēĶ¼2£¬ŌŚ”÷ABCÖŠ£¬”ĻA=36”ć£¬AB=AC£¬”ĻCµÄĘ½·ÖĻß½»ABÓŚµćD£®
£Ø1£©Ö¤Ć÷µćDŹĒAB±ßÉĻµÄ»Ę½š·Öøīµć£»
£Ø2£©Ö¤Ć÷Ö±ĻßCDŹĒ”÷ABCµÄ»Ę½š·ÖøīĻߣ®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com