
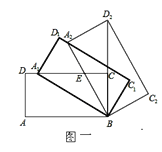
【题目】如图一,矩形ABCD中,AB=m,BC=n,将此矩形绕点B顺时针方向旋转θ(0°<θ<90°)得到矩形A1BC1D1,点A1在边CD上.
(1)若m=2,n=1,求在旋转过程中,点D到点D1所经过路径的长度;
(2)将矩形A1BC1D1继续绕点B顺时针方向旋转得到矩形A2BC2D2,点D2在BC的延长线上,设边A2B与CD交于点E,若![]() ,求
,求![]() 的值.
的值.
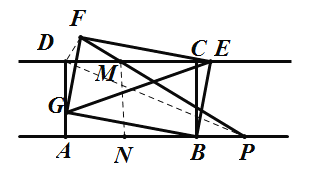
(3)如图二,在(2)的条件下,直线AB上有一点P,BP=2,点E是直线DC上一动点,在BE左侧作矩形BEFG且始终保持![]() ,设AB=
,设AB=![]() ,试探究点E移动过程中,PF是否存在最小值,若存在,求出这个最小值;若不存在,请说明理由.
,试探究点E移动过程中,PF是否存在最小值,若存在,求出这个最小值;若不存在,请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)作A1H⊥AB于H,连接BD,BD1,则四边形ADA1H是矩形.解直角三角形,求出∠ABA1,得到旋转角即可解决问题;
(2)由△BCE∽△BA2D2,推出![]() ,可得CE=
,可得CE=![]() ,由
,由![]() 推出
推出![]() ,推出A1C=
,推出A1C=![]() ,推出BH=A1C=
,推出BH=A1C=![]() ,然后由勾股定理建立方程,解方程即可解决问题;
,然后由勾股定理建立方程,解方程即可解决问题;
(3)当A、P、F,D,四点共圆,作PF⊥DF,PF与CD相交于点M,作MN⊥AB,此时PF的长度为最小值;先证明△FDG∽△FME,得到![]() ,再结合已知条件和解直角三角形求出PM和FM的长度,即可得到PF的最小值.
,再结合已知条件和解直角三角形求出PM和FM的长度,即可得到PF的最小值.
解:(1)作A1H⊥AB于H,连接BD,BD1,则四边形ADA1H是矩形.

∴AD=HA1=n=1,
在Rt△A1HB中,∵BA1=BA=m=2,
∴BA1=2HA1,
∴∠ABA1=30°,
∴旋转角为30°,
∵BD=![]() ,
,
∴D到点D1所经过路径的长度=![]() ;
;
(2)∵△BCE∽△BA2D2,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴A1C=![]() ,
,
∴BH=A1C=![]() ,
,
∴![]() ,
,
∴m4﹣m2n2=6n4,
∴![]() ,
,
∴![]() (负根已舍去).
(负根已舍去).
(3)当A、P、F,D,四点共圆,作PF⊥DF,PF与CD相交于点M,作MN⊥AB,此时PF的长度为最小值;
由(2)可知,![]() ,
,
∵四边形BEFG是矩形,
∴![]() ,
,
∵∠DFG+∠GFM=∠GFM+∠MFE=90°,
∴∠DFG=∠MFE,
∵DF⊥PF,即∠DFM=90°,
∴∠FDM+∠GDM=∠FDM+∠DFM=∠FDM+90°,
∴∠FDG=∠FME,
∴△FDG∽△FME,
∴![]() ,
,
∵∠DFM=90°,![]() ,
,
∴∠FDM=60°,∠FMD=30°,
∴![]() ;
;
在矩形ABCD中,有![]() ,
,
即![]() ,则
,则![]() ,
,
∵MN⊥AB,
∴四边形ANMD是矩形,
∴MN=AD=3,
∵∠NPM=∠DMF=30°,
∴PM=2MN=6,
∴NP=![]() ,
,
∴DM=AN=BP=2,
∴![]() ,
,
∴![]() ;
;


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
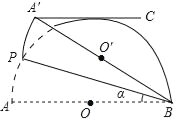
【题目】如图,AB是半圆O的直径,点P(不与点A,B重合)为半圆上一点,将图形沿BP折叠,分别得到点A,O的对应点点A′,O′,过点A′C∥AB,若A′C与半圆O恰好相切,则∠ABP的大小为_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
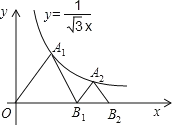
【题目】如图,△OA1B1,△B1A2B2是等边三角形,点A1,A2在函数![]() 的图象上,点B1,B2在x轴的正半轴上,分别求△OA1B1,△B1A2B2的面积.
的图象上,点B1,B2在x轴的正半轴上,分别求△OA1B1,△B1A2B2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 经过原点
经过原点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,顶点为
,顶点为![]() ,对称轴交
,对称轴交![]() 轴于点
轴于点![]() .
.

(1)如图1,求点![]() 的坐标;
的坐标;
(2)如图2,点![]() 为抛物线在第一象限上一点,连接
为抛物线在第一象限上一点,连接![]() 交对称轴于点
交对称轴于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 之间的函数解析式,不要求写出自变量的取值范围;
之间的函数解析式,不要求写出自变量的取值范围;
(3)如图3,在(2)的条件下,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,
,![]() ,
,![]() ,若
,若![]() ,求点
,求点![]() 横坐标
横坐标![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2﹣2ax﹣3a图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于C点,顶点M的纵坐标为4,直线MD⊥x轴于点D.
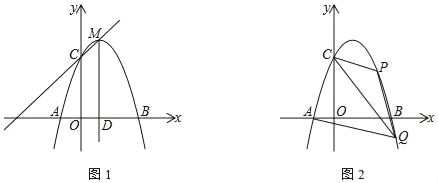
(1)求抛物线的解析式;
(2)如图1,N为线段MD上一个动点,以N为等腰三角形顶角顶点,NA为腰构造等腰△NAG,且G点落在直线CM上.若在直线CM上满足条件的G点有且只有一个时,请直接写出点N的坐标.
(3)如图,点P为第一象限内抛物线上的一点,点Q为第四象限内抛物线上一点,点Q的横坐标比点P的横坐标大1,连接PC、AQ.当PC=![]() AQ时,求S△PCQ的值.
AQ时,求S△PCQ的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解青少年形体情况,现随机抽查了某市若十名初中学生坐必、站姿.走安的好坏情况我们对测评数据作了适当处理(如果一个学生有一种以上:不良姿势.以他最突出的一种作记载) ,并将统计结果绘制了如下两幅不完整的统计图.请你根据图中所给信息解答下列问题:
![]() 求这次抽查一共抽查了多少名学生;
求这次抽查一共抽查了多少名学生;
![]() 请将条形统计图补充完整;
请将条形统计图补充完整;
![]() 如果全市有
如果全市有![]() 万名初中生,那么全市初中生中,三姿良好的学生约有多少名
万名初中生,那么全市初中生中,三姿良好的学生约有多少名

查看答案和解析>>
科目:初中数学 来源: 题型:
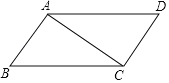
【题目】如图,已知四边形ABCD是平行四边形.
(1)用直尺和圆规作出对角线AC的垂直平分线,分别交AD,BC于E,F;(保留作图痕迹,不写作法)
(2)在(1)作出的图形中,连接CE,AF,若AB=4,BC=8,且AB⊥AC,求四边形AECF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() 中,
中,![]() ,P是斜边AC上一个动点,以即为直径作
,P是斜边AC上一个动点,以即为直径作![]() 交BC于点D,与AC的另一个交点E,连接DE.
交BC于点D,与AC的另一个交点E,连接DE.
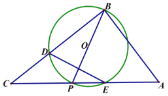
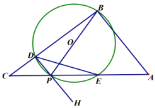
(1)当![]() 时,
时,
①若![]() ,求
,求![]() 的度数;
的度数;
②求证![]() ;
;
(2)当![]() ,
,![]() 时,
时,
①是含存在点P,使得![]() 是等腰三角形,若存在求出所有符合条件的CP的长;
是等腰三角形,若存在求出所有符合条件的CP的长;
②以D为端点过P作射线DH,作点O关于DE的对称点Q恰好落在![]() 内,则CP的取值范围为________.(直接写出结果)
内,则CP的取值范围为________.(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com