
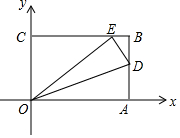
 如图,已知OABC是一张放在平面直角坐标系中的矩形纸片,O为坐标原点,点A(15,0),点C(0,9),在边AB上任取一点D,将△AOD沿OD翻折,使点A落在BC边上,记为点E.
如图,已知OABC是一张放在平面直角坐标系中的矩形纸片,O为坐标原点,点A(15,0),点C(0,9),在边AB上任取一点D,将△AOD沿OD翻折,使点A落在BC边上,记为点E.分析 (1)由题意可得OA的长,然后由折叠的性质,可求得OE的长,然后由勾股定理求得CE的长,再设AD=x,则DE=AD=x,BD=AB-AD=9-x,由BD2+BE2=DE2,可得方程(9-x)2+32=x2,继而求得答案;
(2)首先过点E作EF⊥OA于点F,易得四边形OCEF是矩形,然后由股定理得方程(12-m)2+92=m2,解方程即可求得答案.
解答 解:(1)∵OABC是一张放在平面直角坐标系中的矩形纸片,O为坐标原点,点A(15,0),点C(0,9),
∴OA=BC=15,OC=AB=9,
∵将△AOD沿OD翻折,使点A落在BC边上,记为点E,
∴OE=OA=15,
∴CE=$\sqrt{O{E}^{2}-O{C}^{2}}$=12,
∴BE=BC-CE=3,
设AD=x,则DE=AD=x,BD=AB-AD=9-x,
∵BD2+BE2=DE2,
∴(9-x)2+32=x2,
解得:x=5,
∴AD=5.
故答案为:15,15,12,5;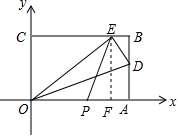 (2)过点E作EF⊥OA于点F,
(2)过点E作EF⊥OA于点F,
∵∠COA=∠BCO=∠OFE=90°,
∴四边形OCEF是矩形,
∴OF=CE=12,EF=OC=9,
设OP=m,则EP=OP=m,PF=12-m,
在Rt△EPF中,PF2+EF2=EP2,
∴(12-m)2+92=m2,
解得:m=$\frac{75}{8}$,
∴点P的坐标为:($\frac{75}{8}$,0).
点评 此题考查了折叠的性质与矩形的性质以及勾股定理.注意利用勾股定理列方程是关键.


科目:初中数学 来源: 题型:选择题
| A. | (0,4) | B. | (0,2) | C. | (0,2)或(0,-2) | D. | (0,4)或(0,-4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+6与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{2}$x交于点A.
如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+6与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{2}$x交于点A.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 7月 | 8月 | 9月 | 10月 | 11月 | 12月 | |
| 销售量 | 8 | 9.3 | 9.8 | 13.4 | 19.7 | 36 |
| 同比增长率 | -2.3% | 6.5% | 5.2% | 15.1% | 20.7% | 35.9% |
| A. | ①③④ | B. | ②③④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 汽车沿一条公路从A地驶往B地所需的时间t与平均速度v | |
| B. | 圆的周长l与圆的半径r | |
| C. | 圆的面积s与圆的半径r | |
| D. | 在电阻不变的情况下,电流强度I与电压U |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一般地,二元一次方程的解可以转化为点的坐标,其中x的值对应为点的横坐标,y的值对应为点的纵坐标,如二元一次方程x-2y=0的解$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$和$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$可以转化为点的坐标A(0,0)和B(2,1).以方程x-2y=0的解为坐标的点的全体叫做方程x-2y=0的图象.
一般地,二元一次方程的解可以转化为点的坐标,其中x的值对应为点的横坐标,y的值对应为点的纵坐标,如二元一次方程x-2y=0的解$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$和$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$可以转化为点的坐标A(0,0)和B(2,1).以方程x-2y=0的解为坐标的点的全体叫做方程x-2y=0的图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
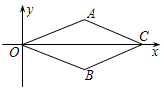 如图,在平面直角坐标系中,菱形OACB的顶点O在原点,点C的坐标为(4,0),点B的纵坐标是-1,则顶点A坐标是( )
如图,在平面直角坐标系中,菱形OACB的顶点O在原点,点C的坐标为(4,0),点B的纵坐标是-1,则顶点A坐标是( )| A. | (2,1) | B. | (1,-2) | C. | (1,2) | D. | (2,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com