
【题目】![]() 是等边三角形,点
是等边三角形,点![]() 在射线
在射线![]() 上,延长
上,延长![]() 至
至![]() ,使
,使![]() .
.


(1)如图(1),当点![]() 为线段
为线段![]() 中点时,求证:
中点时,求证:![]() .
.
(2)如图(2),当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 还成立吗?若成立,请给予证明;若不成立,请说明理由.
还成立吗?若成立,请给予证明;若不成立,请说明理由.
【答案】(1)见解析;(2)![]() 成立,证明见解析.
成立,证明见解析.
【解析】
(1)根据等边三角形的性质可得∠ABC=∠ACB=60°,由等腰三角形“三线合一”的性质可得∠CBD=30°,由CD=AD,CD=CE可得CD=CE,即可得∠CDE=∠CED,利用三角形外角性质可得∠CED=30°,可得∠CBD=∠CED,即可证明DB=DE;
(2)如图,过点![]() 作
作![]() 的平行线
的平行线![]() 交
交![]() 于
于![]() ,根据平行线的性质及等边三角形的性质可证明△CDF是等边三角形,可得CD=DF=CF,利用线段的和差关系可得BC=AC=EF,利用平角的定义可得
,根据平行线的性质及等边三角形的性质可证明△CDF是等边三角形,可得CD=DF=CF,利用线段的和差关系可得BC=AC=EF,利用平角的定义可得![]() =120°,利用SAS可证明
=120°,利用SAS可证明![]() ,即可得DB=DE.
,即可得DB=DE.
(1)∵![]() 是等边三角形
是等边三角形
∴![]()
∵点![]() 为线段
为线段![]() 的中点,
的中点,
∴![]() 平分
平分![]() ,
,![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴∠CBD=∠CED,
∴![]() ;
;
(2)![]() 成立,理由如下:
成立,理由如下:
如图,过点![]() 作
作![]() 的平行线
的平行线![]() 交
交![]() 于
于![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,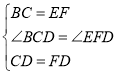 ,
,
∴![]() ,
,
∴![]() .
.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,一次函数
,一次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,且与
,且与![]() 轴以及一次函数
轴以及一次函数![]() 的图像分别交于点
的图像分别交于点![]() 、
、![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.

(1)关于![]() 、
、![]() 的方程组
的方程组![]() 的解为______________.
的解为______________.
(2)关于![]() 的不等式
的不等式![]() 的解集为__________________.
的解集为__________________.
(3)求四边形![]() 的面积;
的面积;
(4)在![]() 轴上是否存在点
轴上是否存在点![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() 为顶点的三角形是直角三角形?若存在,求出点
为顶点的三角形是直角三角形?若存在,求出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学曾有许多重要的成就,其中“杨辉三角” (如图)就是一例. 这个三角形给出了![]() (
(![]() =1,2,3,4,5,6)的展开式(按
=1,2,3,4,5,6)的展开式(按![]() 的次数由大到小顺序排列)的系数规律.例如,第三行的三个数1,2,1,恰好对应
的次数由大到小顺序排列)的系数规律.例如,第三行的三个数1,2,1,恰好对应![]() 展开式中各项的系数;第五行的五个数1,4,6,4,1,恰好对应着
展开式中各项的系数;第五行的五个数1,4,6,4,1,恰好对应着![]() 展开式中各项的系数.
展开式中各项的系数.

(1)![]() 展开式中
展开式中![]() 的系数为________;
的系数为________;
(2)![]() 展开式中各项系数的和为___________.
展开式中各项系数的和为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据媒体报道,在第52届国际速录大赛中我国速录选手获得了7枚金牌、7枚银牌和4枚铜牌,在国际舞台上展示了指尖上的“中国速度”.看到这则新闻后,学生小明和小海很受鼓舞,决定利用业余时间练习打字.经过一段时间的努力,他们的录入速度有了明显的提高.经测试现在小明打140个字所用时间与小海打175个字所用时间相同,小明平均每分钟比小海少打15个字.请求出小明平均每分钟打字的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC右侧作射线CP,∠ACP=![]() (0°<
(0°<![]() <60°),点A关于射线CP的对称点为点D,BD交CP于点E,连接AD,AE.
<60°),点A关于射线CP的对称点为点D,BD交CP于点E,连接AD,AE.

(1)求∠DBC的大小(用含![]() 的代数式表示);
的代数式表示);
(2)在![]() (0°<
(0°<![]() <60°)的变化过程中,∠AEB的大小是否发生变化?如果发生变化,请直接写出变化的范围;如果不发生变化,请直接写出∠AEB的大小;
<60°)的变化过程中,∠AEB的大小是否发生变化?如果发生变化,请直接写出变化的范围;如果不发生变化,请直接写出∠AEB的大小;
(3)用等式表示线段AE,BD,CE之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有些数在我们日常生活中代表一定的含义,如:![]() ,
,![]() ,
,![]() ,
,![]() 等。若在
等。若在![]() 前后各添上一个数字,组成一个新的五位数,则称这个五位数为“恋语数”;如在
前后各添上一个数字,组成一个新的五位数,则称这个五位数为“恋语数”;如在![]() 前添上一个数字
前添上一个数字![]() ,在
,在![]() 后添上一个数字
后添上一个数字![]() ,组成一个新的五位数
,组成一个新的五位数![]() ,则称
,则称![]() 这个五位数为“恋语数”若这个“恋语数”能被
这个五位数为“恋语数”若这个“恋语数”能被![]() 整除,则称这个数为“幸福之家数”.
整除,则称这个数为“幸福之家数”.
(1)请你直接写出![]() 到
到![]() 之间所有的“幸福之家数”;
之间所有的“幸福之家数”;
(2)请你求出能被能被![]() 整除的所有“幸福之家数”的最大值与最小值之差.
整除的所有“幸福之家数”的最大值与最小值之差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市市民晚饭后1小时内的生活方式,调查小组设计了“阅读”、“锻炼”、“看电视”和“其它”四个选项,用随机抽样的方法调查了该市部分市民,并根据调查结果绘制成如下统计图.

根据统计图所提供的信息,解答下列问题:
(1)本次共调查了 名市民;
(2)补全条形统计图;
(3)该市共有480万市民,估计该市市民晚饭后1小时内锻炼的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,假分数可以化为带分数.例如:![]() .在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”,当分子的次数小于分母的次数时,我们称之为“真分式”.例如:
.在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”,当分子的次数小于分母的次数时,我们称之为“真分式”.例如:![]() ,
,![]() 这样的分式就是假分式;
这样的分式就是假分式;![]() ,
,![]() 这样的分式就是真分式.类似的,假分式也可以化为带分式(即整式与真分式和的形式).
这样的分式就是真分式.类似的,假分式也可以化为带分式(即整式与真分式和的形式).
例如:①![]() ;
;
②![]() .
.
(1)将分式![]() 化为带分式;
化为带分式;
(2)若分式![]() 的值为整数,求
的值为整数,求![]() 的整数值;
的整数值;
(3)在代数式![]() 中,若
中,若![]() ,
,![]() 均为整数,请写出
均为整数,请写出![]() 所有可能的取值.
所有可能的取值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com