方程(a-b)x2+(b-c)x+c-a=0的一个解必是 .
【答案】
分析:把原方程进行因式分解,可以求出方程的两个根,其中一个根是1,另一个根用a,b,c的式子表示.
解答:解:(a-b)x
2+(b-c)x+c-a=0,
ax
2-bx
2+bx-cx+c-a=0,
(ax
2-a)-(bx
2-bx)-(cx-c)=0,
a(x+1)(x-1)-bx(x-1)-c(x-1)=0,
(x-1)[a(x+1)-bx-c]=0,
(x-1)[(a-b)x+(a-c)]=0,
∴x
1=1,x
2=-
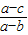
.
∴必有一个根是1.
故本题的答案是1.
点评:本题考查的是一元二次方程的解,根据题目的特点,进行因式分解,就可以求出方程的根,一个根是确定的值,另一个根用含a,b,c的字母表示.

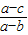 .
.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案