
分析 首先把(-$\frac{1}{3}$)2014化成(-$\frac{1}{3}$)2013×(-$\frac{1}{3}$),然后应用乘法结合律,求出32013×(-$\frac{1}{3}$)2013的值是多少;然后用它和-$\frac{1}{3}$相乘,求出算式32013×(-$\frac{1}{3}$)2014的值是多少即可.
解答 解:32013×(-$\frac{1}{3}$)2014
=32013×[(-$\frac{1}{3}$)2013×(-$\frac{1}{3}$)]
=32013×(-$\frac{1}{3}$)2013×(-$\frac{1}{3}$)
=[3×(-$\frac{1}{3}$)]2013×(-$\frac{1}{3}$)
=(-1)2013×(-$\frac{1}{3}$)
=(-1)×(-$\frac{1}{3}$)
=$\frac{1}{3}$
故答案为:$\frac{1}{3}$.
点评 此题主要考查了幂的乘方法则和积的乘方法则,以及乘法运算定律的应用,要熟练掌握,解答此题的关键是把(-$\frac{1}{3}$)2014化成(-$\frac{1}{3}$)2013×(-$\frac{1}{3}$),进而根据乘法结合律,求出32013×(-$\frac{1}{3}$)2013的值是多少.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 第一次右拐60°,第二次左拐120° | B. | 第一次左拐70°,第二次右拐70° | ||
| C. | 第一次左拐65°,第二次左拐115° | D. | 第一次右拐50°,第二次右拐50° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠AOB=$\frac{1}{2}$∠BOC | B. | ∠AOC=$\frac{1}{2}$∠AOB | C. | ∠AOC=∠BOC | D. | ∠AOB=2∠AOC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
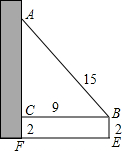 一幢高层住宅楼发生火灾,消防车立即赶到,在距住宅楼9米的B处升起梯搭在火灾窗口(如图),已知云梯长15米,云梯底部距地面2米,发生火灾的住户窗口A离地面有14米.
一幢高层住宅楼发生火灾,消防车立即赶到,在距住宅楼9米的B处升起梯搭在火灾窗口(如图),已知云梯长15米,云梯底部距地面2米,发生火灾的住户窗口A离地面有14米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,抛物线y=a(x-1)2+k(a、k为常数)与x轴交于点A、B,与y轴交于点C,CD∥x轴,与抛物线交于点D.若点A的坐标为(-1,0),则线段OB与线段CD的长度和为5.
如图,在平面直角坐标系中,抛物线y=a(x-1)2+k(a、k为常数)与x轴交于点A、B,与y轴交于点C,CD∥x轴,与抛物线交于点D.若点A的坐标为(-1,0),则线段OB与线段CD的长度和为5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
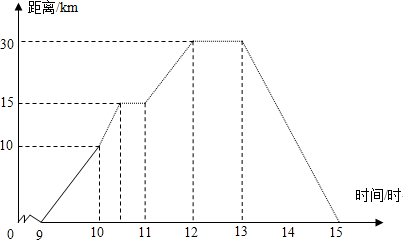
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com