
【题目】我们定义:如图1、图2、图3,在![]() 中,把
中,把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,当
,当![]() 时,我们称
时,我们称![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”,![]() 边
边![]() 上的中线
上的中线![]() 叫做
叫做![]() 的“旋补中线”,点
的“旋补中线”,点![]() 叫做“旋补中心”.图1、图2、图3中的
叫做“旋补中心”.图1、图2、图3中的![]() 均是
均是![]() 的“旋补三角形”.
的“旋补三角形”.
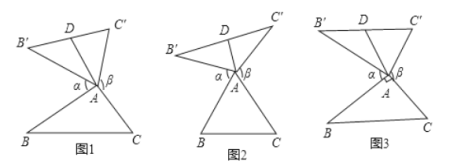
(1)①如图2,当![]() 为等边三角形时,“旋补中线”
为等边三角形时,“旋补中线”![]() 与
与![]() 的数量关系为:
的数量关系为:![]() ______
______![]() ;
;
②如图3,当![]() ,
,![]() 时,则“旋补中线”
时,则“旋补中线”![]() 长为______.
长为______.
(2)在图1中,当![]() 为任意三角形时,猜想“旋补中线”
为任意三角形时,猜想“旋补中线”![]() 与
与![]() 的数量关系,并给予证明.
的数量关系,并给予证明.
【答案】(1)①![]() ;②4;(2)结论:
;②4;(2)结论:![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)①首先证明△ADB'是含有30°的直角三角形,可得AD=![]() AB'即可解决问题;
AB'即可解决问题;
②首先证明△BAC≌△B'AC',根据直角三角形斜边中线等于斜边的一半即可解决问题;
(2)结论:AD=![]() BC.如图1中,延长AD到M,使得AD=DM,连接B'M,C'M,首先证明四边形AC'MB'是平行四边形,再证明△BAC≌△AB'M,即可解决问题;
BC.如图1中,延长AD到M,使得AD=DM,连接B'M,C'M,首先证明四边形AC'MB'是平行四边形,再证明△BAC≌△AB'M,即可解决问题;
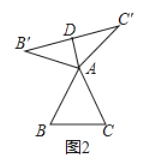
(1)①如图2中,
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案为![]() .
.
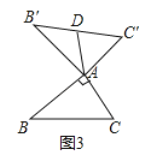
②如图3中,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
故答案为4.
(2)结论:![]() .
.
理由:如图1中,延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∵
,∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,已知,在平面直角坐标系中S△ABC=24,OA=OB,BC=12.

(1)求出三个顶点坐标.
(2)若P点为y轴上的一动点,且△ABP的面积等于△ABC的面积,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系,跨度AB=44米,∠A=45°,AC1=4米,点D2的坐标为(-13,-1.69),则桥架的拱高OH=________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景介绍)勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.
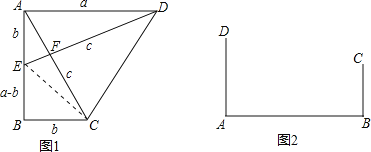
(小试牛刀)把两个全等的直角三角形如图1放置,其三边长分别为a、b、c.显然,∠DAB=∠B=90°,AC⊥DE.请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理:
S梯形ABCD= ,
S△EBC= ,
S四边形AECD= ,
则它们满足的关系式为 ,经化简,可得到勾股定理.
(知识运用)(1)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为 千米(直接填空);
(2)在(1)的背景下,若AB=40千米,AD=24千米,BC=16千米,要在AB上建造一个供应站P,使得PC=PD,请用尺规作图在图2中作出P点的位置并求出AP的距离.
(知识迁移)借助上面的思考过程与几何模型,求代数式![]() 最小值(0<x<16)
最小值(0<x<16)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面材料:
已知点![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() ,
,![]() 两点之间的距离表示为
两点之间的距离表示为![]()
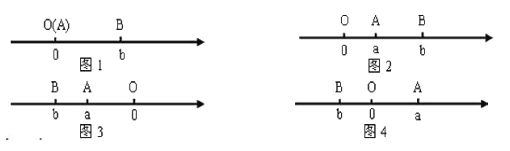
当![]() 两点中有一点在原点时,不妨设点
两点中有一点在原点时,不妨设点![]() 为原点,如图1,
为原点,如图1,![]()
当![]() 两点都不在原点时,
两点都不在原点时,
(1)如图2,点![]() 都在原点的右边,则
都在原点的右边,则![]()
(2)如图3,点![]() 都在原点的左边,则
都在原点的左边,则![]()
(3)如图4,点![]() 都在原点的两边,则
都在原点的两边,则![]()
综上,数轴上![]() 两点的距离
两点的距离![]()
回答下列问题:
(1)数轴上表示-2和5的两点之间的距离是 ;
(2)数轴上表示![]() 和-1的两点
和-1的两点![]() 之间的距离是
之间的距离是![]() ,如果
,如果![]() ,那么
,那么![]() ;
;
(3)拓展:若点![]() 表示的数为
表示的数为![]()
①则当![]() 为 时,
为 时,![]() 与
与![]() 的值相等.
的值相等.
②当![]() 时,整数
时,整数![]() 有 个
有 个
③![]() 的最小值是
的最小值是
④![]() 的最小值是
的最小值是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C为⊙O上一点,将弧BC沿直线BC翻折,使弧BC的中点D恰好与圆心O重合,连接OC,CD,BD,过点C的切线与线段BA的延长线交于点P,连接AD,在PB的另一侧作∠MPB=∠ADC.
(1)判断PM与⊙O的位置关系,并说明理由;
(2)若PC=![]() ,求四边形OCDB的面积.
,求四边形OCDB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有个填写运算符号的游戏:在“![]() □
□![]() □
□![]() □
□![]() ”中的每个“口”内,填入+,-,×,÷中的某一个(可重复使用),然后计算结果.
”中的每个“口”内,填入+,-,×,÷中的某一个(可重复使用),然后计算结果.
(1)计算:![]()
(2)若![]() 口
口![]()
![]() 请推算“口”内的运算符号.
请推算“口”内的运算符号.
(3)在“![]() □
□![]() □
□![]() □
□![]() ”的“口”内填入运算符号后,使计算所得的数最小,直接写出这个最小的数.
”的“口”内填入运算符号后,使计算所得的数最小,直接写出这个最小的数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com