
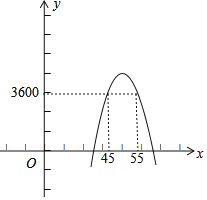
【题目】四川是闻名天下的“熊猫之乡”,每年到大熊猫基地游玩的游客络绎不绝,大学生小张加入创业项目,项目帮助她在基地附近租店卖创意熊猫纪念品.已知某款熊猫纪念物成本为30元/件,当售价为45元/件时,每天销售250件,售价每上涨1元,销量下降10件.
(1)求每天的销售量y(件)与销售单价x(元)之间的函数关系式;
(2)若每天该熊猫纪念物的销售量不低于240件的情况下,当销售单价为多少元时,每天获取的利润最大?最大利润是多少?
(3)小张决定从这款纪念品每天的销售利润中捐出150元给希望工程,为了保证捐款后这款纪念品每天剩余利润不低于3600元,试确定该熊猫纪念物销售单价的范围.
【答案】(1)为y=﹣10x+700;(2)46元时每天获取的利润最大利润是3840元;(3)45≤x≤55.
【解析】
(1)根据每上涨1元,销量下降10件即可求解;
(2)根据每天获得利润等于单件利润乘以销售量列出二次函数,再根据二次函数的性质即可求解;
(3)根据每天剩余利润不低于3600元和二次函数图象即可求解.
解:(1)根据题意,得
y=250﹣10(x﹣45)=﹣10x+700.
答:每天的销售量y(件)与销售单价x(元)之间的函数关系式为y=﹣10x+700.
(2)销售量不低于240件,得﹣10x+700≥240
解得x≤46,
∴30<x≤46.
设销售单价为x元时,每天获取的利润是w元,根据题意,得
w=(x﹣30)(﹣10x+700)
=﹣10x2+1000x﹣21000
=﹣10(x﹣50)2+4000
∵﹣10<0,
所以x<50时,w随x的增大而增大,
所以当x=46时,w有最大值,
w的最大值为﹣10(46﹣50)2+4000=3840.
答:销售单价为46元时,每天获取的利润最大,最大利润是3840元.
(3)根据题意,得
w﹣150=﹣10x2+1000x﹣21000﹣150=3600
即﹣10(x﹣50)2=﹣250
解得x1=55,x2=45,
根据图象得,当45≤x≤55时,捐款后每天剩余利润不低于3600元.


科目:初中数学 来源: 题型:
【题目】已知布袋中有红、黄、蓝色小球各一个,用画树状图或列表的方法求下列事件的概率.
(1)如果摸出第一个球后,不放回,再摸出第二球,求摸出的球颜色是“一黄一蓝”的概率.
(2)随机从中摸出一个小球,记录下球的颜色后,把球放回,然后再摸出一个球,记录下球的颜色,求得到的球颜色是“一黄一蓝”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
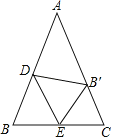
【题目】如图,在等腰△ABC中,AB=AC,点D和点E分别在AB和BC上,连接DE,将△BDE沿DE翻折,点B的对应点B′刚好落在AC上,若AB'=2B'C,AB=3![]() ,BC=6,则BE的长为( )
,BC=6,则BE的长为( )
A.3B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 的半径为1,按如下步骤作图:
的半径为1,按如下步骤作图:

①以![]() 上的点A为圆心,1为半径画弧交
上的点A为圆心,1为半径画弧交![]() 于点B;
于点B;
②依次在![]() 上取点C和D,使得
上取点C和D,使得![]() ;
;
③分别以点A和D为圆心,AC长为半径画弧交于点E;
④以点A为圆心,OE长为半径画弧交![]() 于点F.
于点F.
则以下说法不正确的是( )
A.AC=![]() B.AF
B.AF![]() C.∠ACF=45°D.∠BEO=30°
C.∠ACF=45°D.∠BEO=30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A、B的坐标分别为A(8,0)和B(0,6),点P为x轴负半轴上的一个动点,画△ABP的外接圆,圆心为M,连结BM并延长交圆于点C,连结CP.
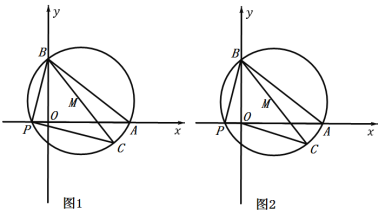
(1)求证:.∠OBP=∠ABC
(2)当![]() 的直径为14时,求点P的坐标.
的直径为14时,求点P的坐标.
(3)如图2,连结OC,求OC的最小值和OC达到最小值时△ABP的外接圆圆心M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
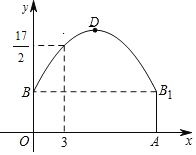
【题目】如图隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=![]() 表示,且抛物线上的点C到OB的水平距离为3m,到地面OA的距离为
表示,且抛物线上的点C到OB的水平距离为3m,到地面OA的距离为![]() m.
m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生阅读课外书籍的情况,某研究小组随机采访该校九年级的20位同学,得到这20位同学阅读课外书册数的统计信息,数据如下:
册数 | 0 | 2 | 3 | 5 | 6 | 8 | 10 |
人数 | 1 | 2 | 4 | 8 | 2 | 2 | 1 |
(1)这20位同学阅读课外书册数的众数是 册,中位数是 册;
(2)若该校九年级有600名学生,试估计该校九年级学生阅读课外书的总册数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+ax+a﹣2=0.
(1)若该方程的一个根为1,求a的值及方程的另一个根;
(2)二次函数y=x2+ax+a﹣2的图象与x轴有交点吗?有几个交点?为什么?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD延长线交于点F,且∠AFB=∠ABC.
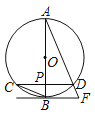
(1)求证:直线BF是⊙O的切线;
(2)若CD=2![]() ,BP=1,求⊙O的半径.
,BP=1,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com