
【题目】在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中.面积最大的三角形的斜边长是_____.
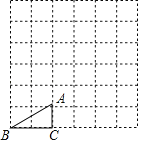
【答案】5![]()
【解析】
根据相似三角形的性质确定两直角边的比值为1:2,以及6×6网格图形中,最长线段为6![]() ,进行尝试,可确定
,进行尝试,可确定![]() 、
、![]() 、
、![]() 为边的这样一组三角形满足条件.
为边的这样一组三角形满足条件.
解:∵在Rt△ABC中,AC=1,BC=2,
∴AB=![]() ,AC:BC=1:2,
,AC:BC=1:2,
∴与Rt△ABC相似的格点三角形的两直角边的比值为1:2,
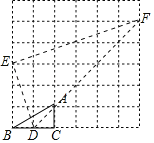
若该三角形最短边长为4,则另一直角边长为8,但在6×6网格图形中,最长线段为6![]() ,但此时画出的直角三角形为等腰直角三角形,从而画不出端点都在格点且长为8的线段,故最短直角边长应小于4,在图中尝试,可画出DE=
,但此时画出的直角三角形为等腰直角三角形,从而画不出端点都在格点且长为8的线段,故最短直角边长应小于4,在图中尝试,可画出DE=![]() ,EF=2
,EF=2![]() ,DF=5
,DF=5![]() 的三角形,
的三角形,
∵![]() =
=![]() =
=![]() =
=![]() ,
,
∴△ABC∽△DEF,
∴∠DEF=∠C=90°,
∴此时△DEF的面积为:![]() ×2
×2![]() ÷2=10,△DEF为面积最大的三角形,其斜边长为:5
÷2=10,△DEF为面积最大的三角形,其斜边长为:5![]() .
.
故答案为:5![]() .
.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点P在BA的延长线上,PA=AO,PD与⊙O相切于点D,BC⊥AB交PD的延长线于点C,若⊙O的半径为1,则BC的长是( )
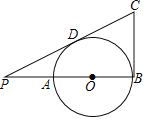
A.1.5B.2C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2018·洛宁县模拟)如图1,正△ABC的边长为4,点P为BC边上的任意一点,且∠APD=60°,PD交AC于点D,设线段PB的长度为x,图1中某线段的长度为y,y与x的函数关系的大致图象如图2,则这条线段可能是图1中的( )
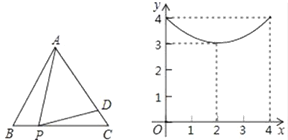
图1 图2
A.线段ADB.线段APC.线段PDD.线段CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,![]() ,点E为BC的中点,以CD为直径在正方形外部作半圆CFD,点F为半圆的中点,连接
,点E为BC的中点,以CD为直径在正方形外部作半圆CFD,点F为半圆的中点,连接![]() ,图中阴影部分的面积是( )
,图中阴影部分的面积是( )
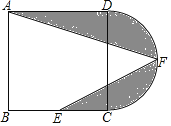
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 和
和![]() 的图象相交于点
的图象相交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(1)求反比例函数的表达式;
(2)设一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的另一个交点为
的图象的另一个交点为![]() ,连接
,连接![]() ,求
,求![]() 的面积.
的面积.
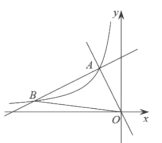
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AC=BC=m,D是AB边上的一点,将∠B沿着过点D的直线折叠,使点B落在AC边的点P处(不与点A,C重合),折痕交BC边于点E.
(1)特例感知 如图1,若∠C=60°,D是AB的中点,求证:AP=![]() AC;
AC;
(2)变式求异 如图2,若∠C=90°,m=6![]() ,AD=7,过点D作DH⊥AC于点H,求DH和AP的长;
,AD=7,过点D作DH⊥AC于点H,求DH和AP的长;
(3)化归探究 如图3,若m=10,AB=12,且当AD=a时,存在两次不同的折叠,使点B落在AC边上两个不同的位置,请直接写出a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E在边AB上,BE=1,∠DAM=45°,点F在射线AM上,且AF=![]() ,过点F作AD的平行线交BA的延长线于点H,CF与AD相交于点G,连接EC、EG、EF.下列结论:①△ECF的面积为
,过点F作AD的平行线交BA的延长线于点H,CF与AD相交于点G,连接EC、EG、EF.下列结论:①△ECF的面积为![]() ;②△AEG的周长为8;③EG2=DG2+BE2;其中正确的是( )
;②△AEG的周长为8;③EG2=DG2+BE2;其中正确的是( )
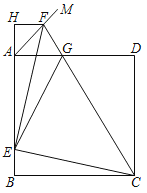
A.①②③B.①③C.①②D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点D是边BC上一动点(不与B、C重合),
,点D是边BC上一动点(不与B、C重合),![]() ,DE交AC于点E,且
,DE交AC于点E,且![]() .下列结论:①
.下列结论:①![]() ∽
∽![]() ;②当
;②当![]() 时,
时,![]() 与
与![]() 全等;③
全等;③![]() 为直角三角形时,BD等于8或
为直角三角形时,BD等于8或![]() .其中正确的有__________.(选填序号)
.其中正确的有__________.(选填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E在BC边上,连接AE,∠DAE的平分线AG与CD边交于点G,与BC的延长线交于点F.设![]() =λ(λ>0).
=λ(λ>0).
(1)若AB=2,λ=1,求线段CF的长.
(2)连接EG,若EG⊥AF,
①求证:点G为CD边的中点.
②求λ的值.
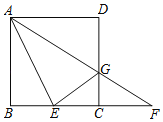
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com