
能够成为直角三角形三条边长的三个正整数,我们称之为勾股数,观察下列表格所给的三个数a,b,c,a<b<c.

(1)试找出它们的共同点,并证明你的结论;
(2)写出当a=17时,b,c的值.
(1)这些勾股数的共同特点是:①以上各组数均满足a2+b 2=c2;②最小数(a)32=9=4+5,52=25=12+13,72=49=24+25,…
2=c2;②最小数(a)32=9=4+5,52=25=12+13,72=49=24+25,…
由以上特点,我们可以猜想这样一个结论:设m是大于1的奇数,将m2拆分为两个连续的整数之和,即m2=n+(n+1),则m,n,n+1就构成一组勾股数.
证明:∵ m2=n+(n+1),∴ m2+n2=2n+1+n2=(n+1)2.根据勾股定理的逆定理,m,n,n+1能够成为直角三角形的三边长.∴ m,n,n+1是一组勾股数.
(2)运用上面得出的结论,当a=17时,∵ 172=289=144+145,∴ b=144,c=145.


科目:初中数学 来源: 题型:
图(A)、图(B)、图(C)是三张形状、大小 完全相同的方格纸,方格纸中的每个小正方形的边长均为
完全相同的方格纸,方格纸中的每个小正方形的边长均为 1.请在图(A)、图(B)、图(C)中,分别画出符合要求的图形,所画图形各顶点必须与方格纸中的小正方形顶点重合.
1.请在图(A)、图(B)、图(C)中,分别画出符合要求的图形,所画图形各顶点必须与方格纸中的小正方形顶点重合.
具体要求如下:
(1)画一个底边长为4,面积为8的等腰三角形;
(2)画一个面积为10的等腰直角三角形;
(3)画一个一边长为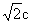 ,面积为6的等腰三角形.
,面积为6的等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,A、B、C为平行四边形的三个顶点,且A、B、C三个顶点的坐标分别为(3,3),(6,4),(4,6).
(1)请直接写出这个平行四边形的第四个顶点坐标;
(2)求此平行四边形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
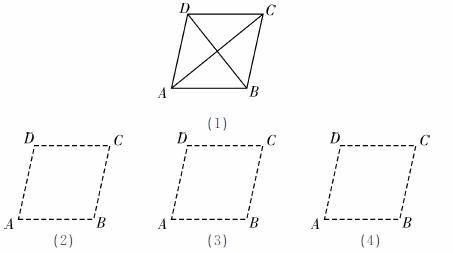
如图,有一张菱形纸片ABCD,AC=8,BD=6.
(1)请沿着AC剪一刀,把它分成两部分,把剪刀的两部分拼成一个平行四边形,在图(2)中用实数画出你所拼成的平行四边形;若沿着BD剪开,请在图(3)中用实线画出拼成的平行四边形;并直接写出这两个平行四边形的周长.
(2)沿着一条直线剪开,拼成与上述两种都不全等的平行四边形,请在图(4)中用实线画出拼成的平行四边形.(注:上述所画的平行四边形都不能与原菱形全等)
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读材料:设一元二次方程ax2+bx+c=0(a≠0)的两根为x1,x2,则两根与方程系数之间有如下关系:x1+x2=﹣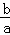 ,x1•x2=
,x1•x2= .
.
根据该材料填空:已知x1,x2是方程x2+6x+3=0的两实数根,则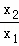 +
+ 的值为
的值为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com