
【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°. 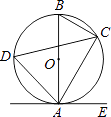
(1)求∠ABC的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧AC的长.
【答案】
(1)解:∵∠ABC与∠D都是弧AC所对的圆周角,
∴∠ABC=∠D=60°
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°.
∴∠BAC=30°,
∴∠BAE=∠BAC+∠EAC=30°+60°=90°,
即BA⊥AE,
∴AE是⊙O的切线
(3)解:如图,连接OC,
∵∠ABC=60°,
∴∠AOC=120°,
∴劣弧AC的长为 ![]() .
.
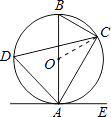
【解析】(1)由圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,即可求得∠ABC的度数;(2)由AB是⊙O的直径,根据半圆(或直径)所对的圆周角是直角,即可得∠ACB=90°,又由∠BAC=30°,易求得∠BAE=90°,则可得AE是⊙O的切线;(3)首先连接OC,易得△OBC是等边三角形,则可得∠AOC=120°,由弧长公式,即可求得劣弧AC的长.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】有三张正面分别标有数字:﹣1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线y= ![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在股市交易中,每买、卖一次需付交易款的千分之七点五作为交易费用,某投资者以每股10元的价格买入某股票1 000股,下表为第一周内每日该股票的涨跌情况(单位:元).
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 | +2 | +1.5 | -0.5 | -4.5 | +2.5 |
(1)星期三收盘时,每股是多少元?
(2)本周内每股最高价是多少元?最低价是多少元?
(3)若该投资者在星期五收盘前将股票全部卖出,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两组卡片共5张,A中三张分别写有数字2,4,6,B中两张分别写有3,5.它们除了数字外没有任何区别.
(1)随机地从A中抽取一张,求抽到数字为2的概率;
(2)随机地分别从A、B中各抽取一张,请你用画树状图或列表的方法表示所有等可能的结果,现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
(3)如果不公平请你修改游戏规则使游戏规则对甲乙双方公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图长方形MNPQ是菜市民健身广场的平面示意图,它是由6个正方形拼成的长方形,中间最小的正方形A的边长是1,观察图形特点可知长方形相对的两边是相等的(如图中MN=PQ).正方形四边相等.请根据这个等量关系,试计算长方形MNPQ的面积,结果为 .
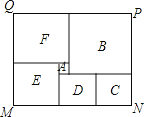
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知关于x的方程kx=11﹣2x有整数解,则负整数k的值为 .
(2)若a+b+c=0,且a>b>c,以下结论:
①a>0,c>0;
②关于x的方程ax+b+c=0的解为x=1;
③a2=(b+c)2;
④![]() 的值为0或2;
的值为0或2;
⑤在数轴上点A、B、C表示数a、b、c,若b<0,则线段AB与线段BC的大小关系是AB>BC.
其中正确的结论是 (填写正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.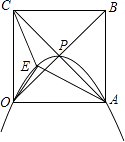
(1)建立适当的平面直角坐标系,
①直接写出O、P、A三点坐标;
②求抛物线L的解析式;
(2)求△OAE与△OCE面积之和的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括O、B),做MN⊥DM,垂足为M,交∠CBE的平分线于点N.
(1)求点C的坐标;
(2)求证:MD=MN;
(3)如图(2),连接DN交BC于F,连接FM,探究线段MF、CF、OM之间有什么数量关系?并证明你的结论.
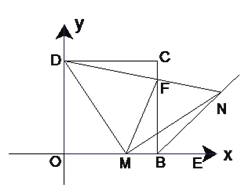
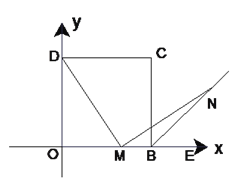
图(1) 图(2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com