
 如图,直线y=mx(m≠0)与双曲线y=$\frac{n}{x}(n≠0)$相交于A(-1,3)、B两点,过点B作BC⊥x轴于点C,连接AC,则△ABC的面积为( )
如图,直线y=mx(m≠0)与双曲线y=$\frac{n}{x}(n≠0)$相交于A(-1,3)、B两点,过点B作BC⊥x轴于点C,连接AC,则△ABC的面积为( )| A. | 3 | B. | 1.5 | C. | 4.5 | D. | 6 |
分析 因为直线与双曲线的交点坐标就是直线解析式与双曲线的解析式联立而成的方程组的解,故求出直线解析式与双曲线的解析式,然后将其联立解方程组,得点B与C的坐标,
再根据三角形的面积公式及坐标的意义求解.
解答 解:∵直线y=mx(m≠0)与双曲线y=$\frac{n}{x}(n≠0)$相交于A(-1,3),
∴-m=3,$\frac{n}{-1}=3$,
∴m=-3,n=-3,
∴直线的解析式为:y=-3x,双曲线的解析式为:y=-$\frac{3}{x}$
解方程组$\left\{\begin{array}{l}{y=-3x}\\{y=-\frac{3}{x}}\end{array}\right.$ 得:$\left\{\begin{array}{l}{{x}_{1=-1}}\\{{y}_{1}=3}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=1}\\{{y}_{2}=-3}\end{array}\right.$
则点A的坐标为(-1,3),点B的坐标为(1,-3)
∴点C的坐标为(1,0)
∴S△ABC=$\frac{1}{2}$×1×(3+3)=3
故:选A
点评 本题考查了反比例函数与一次函数的交点问题,解题的关键是理解函数的图象的交点与两函数解析式之间的关系.


科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | -3 | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源:2017届江苏省宜兴市宜城环科园教学联盟九年级下学期第一次质量检测数学试卷(解析版) 题型:判断题
做服装生意的王老板经营甲、乙两个店铺,每个店铺在同一段时间内都能售出A、B两种款式的服装合计30件,并且每售出一件A款式和B款式服装,甲店铺获利润分别为30元和35元,乙店铺获利润分别为26元和36元.某日,王老板进A款式服装36件,B款式服装24件,并将这批服装分配给两个店铺各30件.
(1)怎样将这60件服装分配给两个店铺,能使两个店铺在销售完这批服装后所获利润相同?
(2)怎样分配这60件服装能保证在甲店铺获利润不小于950元的前提下,王老板获利的总利润最大?最大的总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,为固定电线杆AC,在离地面高度为6m的A处引拉线AB,使拉线AB与地面上的BC的夹角为48°,则拉线AB的长度约为( )
如图,为固定电线杆AC,在离地面高度为6m的A处引拉线AB,使拉线AB与地面上的BC的夹角为48°,则拉线AB的长度约为( )| A. | 6.7m | B. | 7.2m | C. | 8.1m | D. | 9.0m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
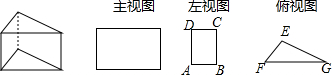
| A. | 6cm | B. | 3$\sqrt{2}$cm | C. | 3cm | D. | 6$\sqrt{2}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x$≤\frac{1}{2}$且x≠1 | B. | x$≥\frac{1}{2}$且x≠1 | C. | x$>\frac{1}{2}$且x≠1 | D. | x$<\frac{1}{2}$且x≠1 |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年山东省淄博市(五四学制)六年级下学期第一次月考数学试卷(解析版) 题型:判断题
先阅读下面例题的解答过程,再解答后面的问题:
例:已知代数式9-6y-4y2=7,求2y2+3y+7的值.
解:由9-6y-4y2=7,得-6y-4y2=7-9,即6y+4y2=2,
因此3y+2y2=1,所以2y2+3y+7=1+7=8.
问题:已知代数式14x+5-21x2=-2,求6x2-4x+5的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com