在一个三位数的百位和十位之间插入:0,1,2,…,9中的一个数码得到的四位数恰是原三位数的9倍,那么这样的三位数中最小的是________,最大的是________.
125 675
分析:设原3位数及插入的数为未知数,其中3位数用3个字母表示,根据得到的四位数恰是原三位数的9倍,得到关系式,得到其余数字与不变的个位和十位数字之间的关系,根据后2位数不超过99判断可能的情况,进而判断百位数字,即可求解.
解答:设这个数是
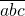
,插入的数是K,那么就有
1000a+100K+10b+c=9(100a+10b+c),整理得25(a+K)=2(10b+c),
∴10b+c是25的倍数,
∵10b+c≤99,
∴10b+c=25,50或75,
当10b+c=25时,a+K=2,a最小为1,∴最小值为125,
当10b+c=75时,a+K=6,a最大为6,∴最大值为675.
故答案为:125;675.
点评:考查学生的推理能力;用到的知识点为:4位数=千位上的数字×1000+百位上的数字×100+10×十位上的数字+个位数字;注意应得到变化的数量与不变的数量之间的关系式.

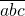 ,插入的数是K,那么就有
,插入的数是K,那么就有
