
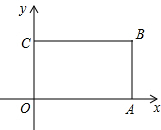
 如图,矩形OABC中,点A,点C分别在x轴,y轴上,D为边BC上的一动点,现把△OCD沿OD对折,C点落在点P处.已知点B的坐标为(2$\sqrt{3}$,2).
如图,矩形OABC中,点A,点C分别在x轴,y轴上,D为边BC上的一动点,现把△OCD沿OD对折,C点落在点P处.已知点B的坐标为(2$\sqrt{3}$,2).分析 (1)依照题意画出图形,根据点D的坐标结合矩形的性质即可得出四边形OCDP是正方形,由此即可得出点P的坐标;
(2)由OP的长度为定值,可知点P的运动轨迹为以2为半径的圆弧,结合点B的坐标借助于特殊角的三角函数值得出∠COP=120°,再套用弧长公式即可得出结论;
(3)取点E(0,4),过点E作⊙O(弧CP段)的切线EP′,切点为P′,连接PP′,找出点P、P′的坐标,利用待定系数法求出k的值,再结合图形即可得出结论.
解答 解:(1)如图1,当D点坐标为(2,2)时,CD=2,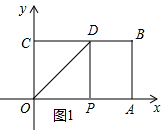
∵OC=2,且四边形OABC为矩形,
∴四边形OCDP是正方形,
∴OP=2,
∴点P的坐标为(2,0).
(2)如图2,∵在运动过程中,OP=OC始终成立,
∴OP=2为定长,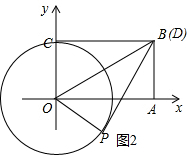
∴点P在以点O为圆心,以2为半径的圆上.
∵点B的坐标为(2$\sqrt{3}$,2),
∴tan∠COB=$\frac{BC}{OC}$=$\sqrt{3}$,
∴∠COB=60°,∠COP=120°,
∴l=$\frac{120°}{360°}$×2π×2=$\frac{4}{3}$π.
(3)在图2的基础上,取点E(0,4),过点E作⊙O(弧CP段)的切线EP′,切点为P′,连接PP′,如图3所示.
∵OE=4,OP′=2,
∴sin∠OEP′=$\frac{OP′}{OE}$=$\frac{1}{2}$,
∴∠OEP′=30°,
∴∠EOP′=60°.
∵∠COP=120°,
∴∠POP′=60°.
∵OP=OP′=60°,
∴△OPP′为等边三角形,
∵OP=2,
∴P($\sqrt{3}$,-1),P′($\sqrt{3}$,1).
当点P在直线y=kx+4上时,有-1=$\sqrt{3}$k+4,
∴k=-$\frac{5\sqrt{3}}{3}$;
当点P′在直线y=kx+4上时,有1=$\sqrt{3}$k+4,
∴k=-$\sqrt{3}$.
综上可知:若点P落在同一条直线y=kx+4上的次数为2次,则k的取值范围为-$\frac{5\sqrt{3}}{3}$≤k<-$\sqrt{3}$.
点评 本题考查了正方形的判定与性质、特殊角的三角函数以及待定系数法求函数解析式,解题的关键是:(1)找出四边形OCDP是正方形;(2)找出点P的运动轨迹为圆弧;(3)求出点P、P′的坐标.本题属于中档题,难度不大,解决该题型题目时,依照题意画出图形,利用数形结合解决问题是关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com