
����Ŀ��3�·ݣ�ijƷ�Ƴ�����ʽ�������ۣ�3 ��1�յ�������Ϊ10����3��2�յ�������Ϊ35�����Ժ�ÿ�����������ǰһ���25����ֱ�����������ﵽ������������ʼ�����½������ˣ�ÿ�����������ǰһ����15����ֱ��3��31��������Ϊ0�����Ʒ�Ƴ��µ�������Ϊp����������������Ϊn���գ���p��n֮��Ĺ�ϵ��ͼ��ʾ��
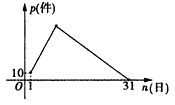
��1����3�� ��ʱ,�����������.
��2��д��p����n�ĺ�����ϵʽ��ע��n ��ȡֵ��Χ����
��3�����о���������Ʒ�Ƴ��µ�����������150����ʱ��Ϊ��Ʒ�Ƴ��µ������ڣ����ʣ���Ʒ�Ƴ��±�����������������Ƕ����죿
���𰸡���1��12
��2��p����n�ĺ�����ϵʽ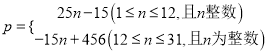
��3����Ʒ�Ƴ��±������������������14��.
����������1����Ϊ5��1����������Ϊ10����5��2����������Ϊ35�����Ժ�ÿ�����������ǰһ���25����ֱ�����������ﵽ������������ʼ�����½������ˣ�ÿ�����������ǰһ����15����ֱ��5��31��������Ϊ0������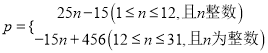
��2����1��n��12ʱ��12��n��31��������г�����ʽ���ֱ����n��ȡֵ��Χ���ɣ�
��3����12��Ϊ�磬ǰ���������Ȳ����� �� 1��n��12ʱ������a1=10��ĩ��a12=285������ k1=12 ���� �� s1=��10+285����![]() =1770 �� 12��n��31ʱ������a13=270��ĩ��a31=0������ k2=19 ���� �� s1=270��
=1770 �� 12��n��31ʱ������a13=270��ĩ��a31=0������ k2=19 ���� �� s1=270��![]() =2565���������ͼ��ɣ�
=2565���������ͼ��ɣ�
�⣺(1)��3��x�����һ�����������ӵ����ڣ�������ã�
![]() �����
�����![]()
��2���ɣ�1����![]() ��
��![]()
��3����![]() ��
��![]() �����
�����![]() ������ʵ�����ڣ�
������ʵ�����ڣ�
Ӧ��7�����㣬�˶�ʱ��������Ϊ12-7+1=6��
��![]() ���ʴ˶�������Ϊ
���ʴ˶�������Ϊ
20-12=8�졣���6+8=14��
���㾦�����⿼����һ�κ��������ã�һ�κ�����ͼ�����������ã����һ�κ����Ľ���ʽ�����ã����ʱ�������������ϸ�۲�ͼ�����÷ֶκ�����������ǽ���ؼ���


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
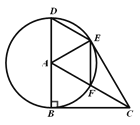
����Ŀ����Rt��ABC�У���ABC=90�㣬�Ե�AΪԲ�ģ�ABΪ�뾶������A��AC�ڵ�F����BA���ӳ����ڵ�D������D��AC��ƽ���߽���A�ڵ�E������AE��CE��EF��
����֤��CE��AE;
�Ƶ���CAB���ڶ��ٶ�ʱ���ı���ADEFΪ���Σ�������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
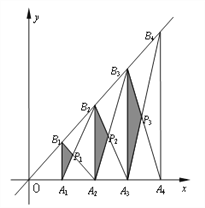
����Ŀ����ͼ����֪A1��A2��������An��An��1��x���ϵĵ㣬��OA1��A1A2��A2A3��������AnAn��1��1���ֱ����A1��A2��������An��An��1��x��Ĵ��߽�ֱ��y��2x�ڵ�B1��B2��������Bn��Bn��1������A1B2��B1A2��A2B3��B2A3��������AnBn��1��BnAn��1�������ཻ�ڵ�P1��P2��P3��������Pn����A1B1P1����A2B2P2����������AnBnPn���������ΪS1��S2��������Sn����SnΪ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��ƽ���ӱ���ÿ��ֻ�ܷ����ű���������һ�ű�2���ӣ����������һ���ӣ���������3�ű�������________���ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���OAB�ǵȱ������Σ�OΪ����ԭ�㣬��A�������ǣ�3��0������C��OA����OC=1������BC��һ����P�ӵ�A������������A��B��O�ķ������յ�O�˶����ǵ�P�ƶ���·��Ϊm��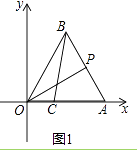
��1������P���߶�AB���˶�ʱ������OP���������BPO�ա�OCB��mֵ��
��2������PC�����OPC�����s����m�ĺ�������ʽ��
��3����ͼ2������P����AB�Ĵ���l������ֱ��lΪ�Գ��ᣬ���߶�AC�ĶԳ��߶�A1C1 �� ��д���ڵ�P���˶������У��߶�A1C1��y���н���ʱm��ȡֵ��Χ��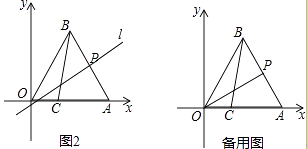
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
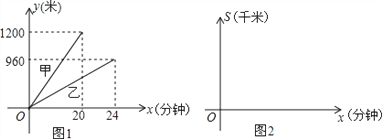
����Ŀ��A,B,C����������һ��ֱ�߹�·��,��,�Ҷ��˷ֱ��A,B����ͬʱ�����ع�·���ٲ��е�C��,����������صľ���y(��)�����ʱ��x(����)����ͼ����ͼ1��ʾ.
(1)�IJ����ٶ�Ϊ ��/����,�ҵIJ����ٶ�Ϊ ��/����,A,B����֮��ľ���Ϊ �ף�
(2)��������B�صľ���Ϊs(��),����ʱ��x(����),����ͼ(2)�зֱ���,�Ҷ���s��x�ĺ���ͼ��.
(3)���˳����ʱ����B�ؾ������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��100��100Ԫ���°�����Ҵ�Լ0.9������100��Ԫ����������ҵ���һ��ĸ߶�ԼΪ_____���ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ�ڵ��������������У��ס�����ͬѧ��ƽ���ɼ�һ��������ֱ�Ϊ1.5��1.0��������˵����ȷ������ ��
A. ��ͬѧ�ijɼ����ȶ� B. ��ͬѧ�ijɼ����ȶ�
C. �ס�����λͬѧ�ijɼ�һ���ȶ� D. ����ȷ����λͬѧ�ijɼ����ȶ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x0�Ƿ���ax2+2x+c=0��a��0����һ��������M=1��ac��N=��ax0+1��2 �� ��M��N�Ĵ�С��ϵ��ȷ��Ϊ��������
A.M��N
B.M=N
C.M��N
D.��ȷ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com