练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
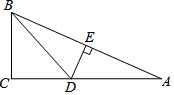
    20．如图，在Rt△ABC中，∠C=90°，把AB对折后，点A与点B重合，折痕为DE，若BC=2，AC=4，则BD=（　　）
    A．$\frac{3}{2}$B．2C．$\frac{5}{2}$D．3

    分析 根据翻折的性质可得BD=AD，设BD=x，表示出CD，然后利用勾股定理列方程求解即可．

    解答 解：∵把AB对折后，点A与点B重合，折痕为DE，
    ∴BD=AD，
    设BD=x，则CD=AC-AD=4-x，
    ∵∠C=90°，
    ∴BC2+CD2=BD2，
    即22+（4-x）2=x2，
    解得x=$\frac{5}{2}$，
    即BD=$\frac{5}{2}$．
    故选C．

    点评 本题考查了翻折变换的性质，勾股定理，主要利用了翻折前后对应边相等，此类题目，利用勾股定理列出方程是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    7．已知关于x的不等式（2a-3b）x＞7a-5b的解集是x＜$\frac{2}{3}$，则关于x的不等式（7a-3b）x＞2a-5b的解集是x＜-$\frac{37}{12}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．“六一”期间，小张购进100只两种型号的文具进行销售，其进价和售价之间的关系如表：
    型号进价（元/只）售价（元/只）
    A型1012
    B型1523
    设小张购进A型文具x只．
    （Ⅰ）当x为何值时，购进这两种文具的进货款恰好为1320元；
    （Ⅱ）当x为何值时，销售这批文具所获利润最大，并且所获利润不超过进货价格的40%，最大利润是多少元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．方程2$\sqrt{1+x}$-$\sqrt{2+2\sqrt{1-{x}^{2}}}$=1的解是x=$\frac{\sqrt{3}}{2}$或x=-$\frac{\sqrt{3}}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

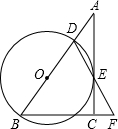    15．如图，在 Rt△ABC中，∠ACB=90°，点D是边AB上一点，以BD为直径的⊙O与边AC相切于点E，连接DE并延长DE交BC的延长线于点F．
    （1）求证：BD=BF；
    （2）若CF=1，$\frac{OA}{BA}$=$\frac{3}{5}$，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．有理数a，b在数轴上的位置如图所示，则|a+b|+|a-b|化简的结果为（　　）
    A．-2bB．-2aC．2bD．0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．用一平面去截一个正方体，能截出梯形，请在如图的正方体中画出．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

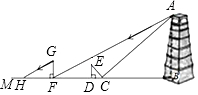    9．如图，小亮、小芳同学想测量一座塔的高度，他们经过观察发现需要两次测量，于是他们首先用平面镜进行测量，方法如下：如图，小芳在小亮和塔之间的直线BM上平放一平面镜，在镜面上做了一个标记，这个标记在直线BM上的对应位置为点C，镜子不动，小亮看着镜面上的标记，来回走动，走到点D时，看到塔顶端点A在镜面中的像与镜面上的标记重合，这时，测得小亮眼睛与地面的高度ED=1.5米，CD=3米；然后，在阳光下，他们用测影长的方法进行了第二次测量，方法如下：如图，小亮从D点沿DM方向走了17米，到达塔影子的末端F点处，此时，测得小亮身高GF的影长FH=4.2米，GF=1.6米，如图，已知AB⊥BM，ED⊥BM，GF⊥CM，其中，测量时所使用的平面镜的厚度忽略不计，请你根据题中的信息，求出塔的高AB的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．某种储蓄的月利率是2%，存入100元本金后，则本息和y（元）与所存月数x之间的关系式为y=2x+100．

    查看答案和解析>>

    同步练习册答案