
分析 (1)原式结合后,相加即可得到结果;
(2)原式利用减法法则变形,结合后相加即可得到结果;
(3)原式利用乘法法则计算即可得到结果;
(4)原式从左到右依次计算即可得到结果;
(5)原式变形后,利用乘法分配律计算即可得到结果;
(6)原式利用乘法分配律计算即可得到结果;
(7)原式逆用乘法分配律计算即可得到结果;
(8)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
(9)原式先计算绝对值及括号中的运算,再计算乘法运算即可得到结果.
解答 解:(1)原式=(-14-16)+(26+8)=-30+34=4;
(2)原式=(-40-28-24-32)+19=-124+19=-105;
(3)原式=-8×6×$\frac{5}{4}$×$\frac{1}{3}$=-20;
(4)原式=-$\frac{1}{2}$×$\frac{4}{3}$×$\frac{5}{4}$×$\frac{5}{6}$=-$\frac{25}{36}$;
(5)原式=(-10+$\frac{1}{21}$)×42=-420+2=-418;
(6)原式=-28-20+33=-15;
(7)原式=-$\frac{3}{10}$×(7+7)=-3;
(8)原式=$\frac{1}{4}$×(-8)-4×$\frac{9}{4}$-1=-2-9-1=-12;
(9)原式=3×$\frac{1}{15}$×0=0.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
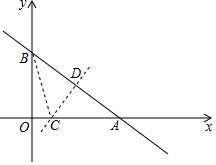 如图,直线y=-$\frac{3}{4}$x+6与x、y轴分别交于点A,B.
如图,直线y=-$\frac{3}{4}$x+6与x、y轴分别交于点A,B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,把半径为2个长度单位的圆形纸片放在数轴上,圆形纸片上的A点对应原点,将圆形纸片沿着数轴无滑动的逆时针滚动一周,点A到达点A′的位置,则点A′表示的数是-4π.
如图所示,把半径为2个长度单位的圆形纸片放在数轴上,圆形纸片上的A点对应原点,将圆形纸片沿着数轴无滑动的逆时针滚动一周,点A到达点A′的位置,则点A′表示的数是-4π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 作图题:如图,正方形网格中的每个小正方形边长都是1,任意连结这些小正方形的顶点,可得到一些线段.请在图中画出△ABC,使得AB=5,AC=$\sqrt{10}$,BC=$\sqrt{17}$.并注明点A、B、C.
作图题:如图,正方形网格中的每个小正方形边长都是1,任意连结这些小正方形的顶点,可得到一些线段.请在图中画出△ABC,使得AB=5,AC=$\sqrt{10}$,BC=$\sqrt{17}$.并注明点A、B、C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com