
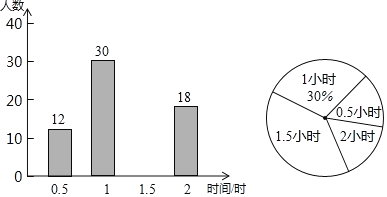
【题目】2019年8月,第18届世界警察和消防员运动会在成都举行.我们在体育馆随机调查了部分市民当天的观赛时间,并用得到的数据绘制了如下不完整的统计图,根据图中信息完成下列问题:
(1)将条形统计图补充完整;
(2)求抽查的市民观赛时间的众数、中位数;
(3)求所有被调查市民的平均观赛时间.
【答案】(1)答案见解析;(2)众数是1.5小时,中位数是1.5小时;(3)1.32小时.
【解析】
(1)根据观赛时间为1小时的人数和所占的百分比可以求得本次调查的人数,从而可以得到观赛时间为1.5小时的人数,进而可以将条形统计图补充完整;
(2)根据(1)中条形统计图中的数据可以得到抽查的市民观赛时间的众数、中位数;
(3)根据条形统计图中的数据可以计算出所有被调查市民的平均观赛时间.
(1)本次调查的人数为:30÷30%=100,
观赛时间为1.5小时的有:100﹣12﹣30﹣18=40(人),
补全的条形统计图如右图所示;
(2)由(1)中的条形统计图可知,
抽查的市民观赛时间的众数、中位数分别是1.5小时、1.5小时;
(3)![]() 1.32(小时),
1.32(小时),
答:所有被调查市民的平均观赛时间是1.32小时.



科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).

A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
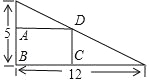
【题目】如图在一块直角三角形铁皮废料的内部剪下一个长方形盒盖 ABCD,其中 AB 和 BC 分别在两直角边上,设AB=x cm,BC 满足关系式:﹣![]() x+12, 长方形盒盖的面积为 y cm2,则 x 的取值为多少时?y 可以取得最大值,最大值是多少?
x+12, 长方形盒盖的面积为 y cm2,则 x 的取值为多少时?y 可以取得最大值,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
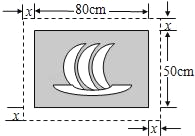
【题目】在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是ycm2,设金色纸边的宽为xcm,要求纸边的宽度不得少于1cm,同时不得超过2cm.
(1)求出y关于x的函数解析式,并直接写出自变量的取值范围;
(2)此时金色纸边的宽应为多少cm时,这幅挂图的面积最大?求出最大面积的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,平面直角坐标系中,抛物线![]() 经过
经过![]() 、
、![]() 、
、![]() .过点
.过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() .点
.点![]() 是四边形
是四边形![]() 的对角线的交点,点
的对角线的交点,点![]() 在
在![]() 轴负半轴上,且
轴负半轴上,且![]() .
.
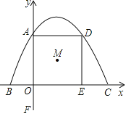
(1)求抛物线的解析式,并直接写出四边形![]() 的形状;
的形状;
(2)当点![]() 、
、![]() 从
从![]() 、
、![]() 两点同时出发,均以每秒
两点同时出发,均以每秒![]() 个长度单位的速度沿
个长度单位的速度沿![]() 、
、![]() 方向运动,点
方向运动,点![]() 运动到
运动到![]() 时
时![]() 、
、![]() 两点同时停止运动.设运动的时间为
两点同时停止运动.设运动的时间为![]() 秒,在运动过程中,以
秒,在运动过程中,以![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形的面积为
四点为顶点的四边形的面积为![]() ,求出
,求出![]() 与
与![]() 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;
(3)在抛物线上是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是梯形?若存在,直接写出点
为顶点的四边形是梯形?若存在,直接写出点![]() 的坐标;不存在,说明理由.
的坐标;不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
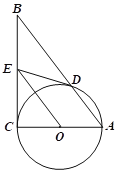
【题目】如图在RtΔABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB,交BC于E.
(1)求证:ED是⊙O的切线;
(2)如果⊙O的半径为1.5,ED=2,求AB的长.
(3)在(2)的条件下,求△ADO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
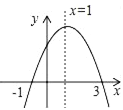
【题目】如图为二次函数y=ax2+bx+c的图象,给出下列说法:
①ab>0;
②方程ax2+bx+c=0的根为x1=﹣1,x2=3;
③a+b+c>0;
④当x>1时,随x值的增大而增大.
其中正确的说法有______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,2),B(1,﹣1),C(3,0).
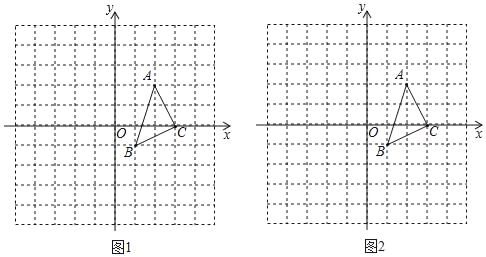
(1)在图1中,画出以点O为位似中心,放大△ABC到原来的2倍的△A1B1C1;
(2)若P(a,b)是AB边上一点,平移△ABC之后,点P的对应点P'的坐标是(a+3,b﹣2),在图2中画出平移后的△A2B2C2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com