
| 画板的边长(dm) | 10 | 20 |
| 出售价(元/张) | 160 | 220 |
|
|
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AB为⊙O的直径,点C为⊙O上的一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.试判断CD与⊙O的位置关系,并说明理由.
如图,AB为⊙O的直径,点C为⊙O上的一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.试判断CD与⊙O的位置关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
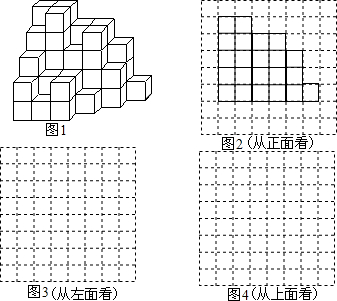 操作题
操作题查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在一旗杆AB的顶端A上系一活动旗帜,在某一时刻,旗杆的影子落在平地BD和一坡度为1:
如图,在一旗杆AB的顶端A上系一活动旗帜,在某一时刻,旗杆的影子落在平地BD和一坡度为1:| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
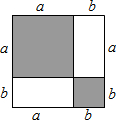 我们分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0,则M<N.利用“作差法”解决下列问题:
我们分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0,则M<N.利用“作差法”解决下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com