
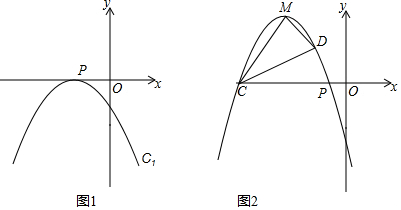
 已知,抛物线C1:y=-$\frac{1}{2}$x2+mx+m+$\frac{1}{2}$.
已知,抛物线C1:y=-$\frac{1}{2}$x2+mx+m+$\frac{1}{2}$.分析 (1)①直接得出点P的坐标;②用配方法确定出抛物线的顶点式方程,即可得出结论
(2)先确定出抛物线C1,C2的解析式,得出此两个函数图形关于x轴对称,从而设出点B的坐标,最后利用等腰直角三角形的性质列出方程,解方程即可得出结论;
(3)方法一:先确定出点C坐标,根据条件确定出四边形的面积是三角形PAC面积的2倍,列出方程即可确定出m.最后代入解析式即可;
方法二:先确定出直线CD解析式,再用到坐标系下的三角形面积公式(水平宽乘以铅垂高的一半建立方程的)分别表示出S△PCD和S△MCD,从而建立方程求解m,再代入解析式即可.
解答 解:(1)①∵抛物线C1:y=-$\frac{1}{2}$x2+mx+m+$\frac{1}{2}$=-$\frac{1}{2}$x2+m(x+1)+$\frac{1}{2}$.
∴当x+1=0时,无论m为何值,抛物线经过顶点P,
∴x=-1,y=0,
∴定点P(-1,0),
故答案为:-1,0;
②抛物线C1:y=-$\frac{1}{2}$x2+mx+m+$\frac{1}{2}$=-$\frac{1}{2}$(x-m)2+$\frac{1}{2}$(m+1)2.
∴M(m,$\frac{1}{2}$(m+1)2),
∴函数C2的关系式为y=$\frac{1}{2}$(x+1)2;
故答案为:y=$\frac{1}{2}$(x+1)2;
(2)如图1所示,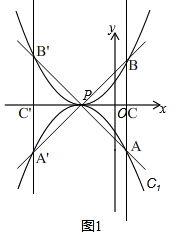
∵抛物线C1:y=-$\frac{1}{2}$x2+mx+m+$\frac{1}{2}$顶点在x轴,则m=-1,
∴抛物线C1:y=-$\frac{1}{2}$x2-x-$\frac{1}{2}$=-$\frac{1}{2}$(x+1)2,P(-1,0),
由②知,函数C2的关系式为y=$\frac{1}{2}$(x+1)2;
∴抛物线C1与C2关于x轴对称,
∵△PAB为等腰直角三角形,
∴直角顶点只能是点P,且PC=BC=AC,
设B(n,$\frac{1}{2}$(n+1)2),
∴C(n,0),BC=$\frac{1}{2}$(n+1)2,
∴PC=|n+1|,
∴$\frac{1}{2}$(n+1)2=|n+1|,
∴n=-1(舍)或n=1或n=-3.
∴直线l的解析式为x=1或x=-3.
(3)方法一:如图2,过点M作ME⊥OC,过点D作DF⊥OC,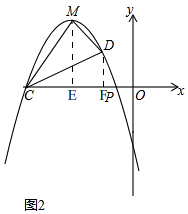
∵抛物线C1:y=-$\frac{1}{2}$x2+mx+m+$\frac{1}{2}$.
∴M(m,$\frac{1}{2}$(m+1)2),P(-1,0),C(2m+1,0),
∵抛物线上点M与点P之间一点D的横坐标为-2,
∴D(-2,-m-$\frac{3}{2}$),
∴S△PCD=$\frac{1}{2}$PC×DF,
∵S△PCD=S△MCD,
S四边形CPDM=S△DFP+S梯形DFEM+S△CEM
=$\frac{1}{2}$×PF×DF+$\frac{1}{2}$(DF+ME)×EF+$\frac{1}{2}$×CE×ME
=2S△PCD=2×$\frac{1}{2}$PC×DF,
∴PF×DF+EF×DF+ME×EF+CE×ME=2PC×DF,
∴DF(PF+EF)+ME(EF+CE)=2PC×DF,
∴DF×PE+ME×CF=2PC×DF,
∴DF×$\frac{1}{2}$PC+ME(PC-PF)=2PC×DF,
∴DF×PC+2ME×PC-2ME×PF=4PC×DF,
∴2ME×PC-3PC×DF=2ME×PF,
∴PC(2ME-3DF)=2ME×PF,
∴[-1-(2m+1)][(m+1)2-3(-m-$\frac{3}{2}$)]=(m+1)2×1,
∴(m+1)(m+4)(2m+3)=0,
∴m=-1(舍)或m=-4或m=-$\frac{3}{2}$,
当m=-4时,二次函数的解析式y=-$\frac{1}{2}$x2-4x-$\frac{7}{2}$.
当m=-$\frac{3}{2}$时,二次函数的解析式y=-$\frac{1}{2}$x2-$\frac{3}{2}$x-1.
方法二,如图,过点M作ME⊥x轴交CD于E,过点D作DF⊥x轴,
∵抛物线C1:y=-$\frac{1}{2}$x2+mx+m+$\frac{1}{2}$.
∴M(m,$\frac{1}{2}$(m+1)2),P(-1,0),C(2m+1,0),
∵抛物线上点M与点P之间一点D的横坐标为-2,
∴D(-2,-m-$\frac{3}{2}$),
∴直线CD解析式为y=$\frac{1}{2}$x-$\frac{1}{2}$(2m+1),
∴E(m,-$\frac{1}{2}$(m+1)
∵S△MCD=$\frac{1}{2}$×CF×ME=$\frac{1}{2}$×[-2-(2m+1)]×[$\frac{1}{2}$(m+1)2+$\frac{1}{2}$(m+1)]=-$\frac{1}{2}$(m+1)(m+2)(m+$\frac{3}{2}$),
S△PCD=$\frac{1}{2}$PC×DF=$\frac{1}{2}$[-1-(2m+1)]×(-m-$\frac{3}{2}$)=(m+1)(m+$\frac{3}{2}$),
∵S△PCD=S△MCD,
∴-$\frac{1}{2}$(m+1)(m+2)(m+$\frac{3}{2}$)=(m+1)(m+$\frac{3}{2}$),
∴(m+1)(m+4)(2m+3)=0,
∴m=-1(舍)或m=-4或m=-$\frac{3}{2}$,
当m=-4时,二次函数的解析式y=-$\frac{1}{2}$x2-4x-$\frac{7}{2}$.
当m=-$\frac{3}{2}$时,二次函数的解析式y=-$\frac{1}{2}$x2-$\frac{3}{2}$x-1.
点评 此题是二次函数综合题,主要考查了二次函数解析式的两种形式的转化,等腰直角三角形的性质,图形面积的计算,解本题的关键是判断出抛物线C1,C2的图象关于x轴对称,(3)列出方程,解本题的难点是(3)方程的处理,计算量比较大,尤其是第三问的方程的处理.注:第三问,方法二,简洁,解方程也比较简单.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:解答题
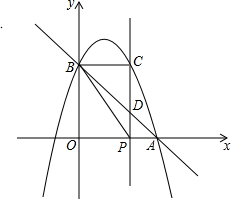 如图,已知抛物线y=-x2+bx+c与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),点P是x轴上一动点,过点P作x轴的垂线交抛物线于点C,交直线AB于点D,设P(x,0).
如图,已知抛物线y=-x2+bx+c与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),点P是x轴上一动点,过点P作x轴的垂线交抛物线于点C,交直线AB于点D,设P(x,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
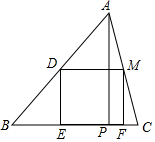 如图,△ABC是一块面积为2700cm2的三角形木板,其中BC=90cm,现在要将这块木板加工成一个正方形的桌面,如图所示,正方形DEFM即是要加工成的桌面,点D、M分别在AB、AC边上,点E、F在BC边上,根据以上数据求出这个正方形桌面的边长.
如图,△ABC是一块面积为2700cm2的三角形木板,其中BC=90cm,现在要将这块木板加工成一个正方形的桌面,如图所示,正方形DEFM即是要加工成的桌面,点D、M分别在AB、AC边上,点E、F在BC边上,根据以上数据求出这个正方形桌面的边长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
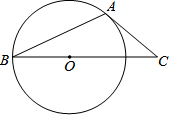 如图,在⊙O中,AB是⊙O的弦,BC经过圆心,∠B=25°,∠C=40°.
如图,在⊙O中,AB是⊙O的弦,BC经过圆心,∠B=25°,∠C=40°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com